再々改訂版 2025/05/28
再改定版 2025/05/24
著者 久米原 栄
- コラッツ予想とは
- 証明の要約
- 以下証明する)
- コラッツ操作を施した場合のタイプ毎の動き
- タイプ遷移図
- タイプ型と、第2桁の偶数・奇数、3桁以上の整数への拡張
- タイプ別の縮小と拡大の概略
- タイプ1の整数を出発点とするとき
- タイプ3の整数を出発点とするとき
- タイプ5の整数を出発点とするとき
- タイプ9の整数を出発点とするとき
- タイプ13の整数を出発点とするとき
- タイプ7の整数を出発点とするとき
- タイプ11の整数を出発点とするとき
- タイプ15の整数を出発点とする時
- 保留として残したものについての検討
- 第2桁の偶数・奇数の割合
- 桁を増やしてみよう
- (3n+1)/2と/2の処理で偶数奇数はどうなるのか
- 拡張列を更に追跡すると
- タイプ7、タイプ11のモデル化
- 15タイプからの遷移
- 15が最小桁から連続する場合についての考察
- タイプ15の連続からの脱却
- 途中にある15についての考察
- 他のタイプから15タイプへの遷移
- 2桁の数について、コラッツ予想が成り立つことの証明
- 結論
コラッツ予想とは
コラッツ予想とは、任意の正の整数を選んで、nが偶数なら2で割り、nが奇数なら3を掛けて1を足すという操作を繰り返すと、どんなnから始めても有限回の操作で1に辿り着くという主張である。
証明の要約
任意の正の整数を16を基数としてan16n+an-116n-1+…+a116+a0と表す(an, an-1, … a1, a0は0から15までの整数とする)。ある任意の正の整数に対して、コラッツ操作を施す時に、それが偶数なら、その偶数が含んでいる因数2の個数分「2で割る」処理をして、奇数を取り出すという処理は、コラッツ操作の前処理として考えることにしよう。こうすると、コラッツ操作の対象となるのは奇数ということになる。もちろん、計算処理の途中で偶数が現れることはある。奇数nに対して、(3n+1)/2の処理をして得られた答えに対して、更に「割る2」の処理が可能ならば、「割る2」の処理をして、答えから因数2を取り除くという一連の処理をコラッツ操作1回分として計算することとする。
コラッツ操作の対象を奇数として、16を基数とする表現で表すと、最小桁によってタイプ分けすることが出来る。つまり、あらゆる正の奇数は、タイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15の8つのタイプに分けることが出来る。
任意の整数にコラッツ操作を施すと、タイプ毎に同じ動きをする。そして、あるタイプから別のタイプに遷移する。どのタイプに遷移するかは第2桁が偶数か奇数かによって決定される。このタイプ遷移をグラフに表すことが出来る。これを本稿ではタイプ遷移図と称している。タイプ遷移図はどのタイプからどのタイプに遷移するかをグラフ化したものとなる。あるタイプから別のタイプに移るときにいくつかの分岐先がある。2つに分岐する場合、4つに分岐する場合、8つに分岐する場合である。
2つに分岐するのはタイプ3、タイプ7、タイプ11、タイプ15である。整数にコラッツ操作を施す場合1回の分岐で通常は3/2倍となる。従って、分岐1回で2つに分岐するだけの場合は基本的には3/2倍される。タイプ3、タイプ7、タイプ11、タイプ15を経由するときには基本的に3/2倍されることになる。4つに分岐される時は最初の分岐は(3n+1)/2の処理による分岐で、後の1回の分岐はタイプ内の内部処理として「割る2」されるだけである。従って、4つに分岐する場合は、「3/2 x 1/2 = 3/4」倍されることになり、分岐によって3/4に縮小することになる。4つに分岐するのはタイプ1と、タイプ9である。8つに分岐する場合は最初の(3n+1)/2の処理と、後2回の「割る2」の内部処理になるので、「3/2 x 1/2 x 1/2 = 3/8」となる。8つに分岐するのはタイプ13である。更にタイプ5に関しては内部処理として「1/2 x 1/2 x 1/2」されるので、3/2と合わせると、3/16倍されることになる。そして、タイプ3に関しては、分岐としてタイプ5あるいはタイプ13に分かれるので、拡張タイプでありながらタイプ5、タイプ13の処理と合わせると総合的には縮小タイプとなる事が分かる。以上のことを元にして分岐を辿ると、タイプ1、タイプ3、タイプ5、タイプ9、タイプ13を起点としてコラッツ操作を施すと全て倍率1以下に収束することが分った。そして、タイプ7、タイプ11についても全て倍率1以下になることが証明できた。更に残ったタイプ15についても、それが有限の整数である限り、やがてタイプ7に変容することが証明できた。従って、全ての整数がコラッツ操作の起点となる整数よりも小さい整数にまで収束することが分かった。更に、2桁の整数の全てがコラッツ操作を繰り返すことで1になることも証明した。したがって小さい整数から順番にコラッツ操作を施していくと、全ての整数が1になることが分かった。
以下証明する)
任意の整数は、16を基数として、an16n+an-116n-1+…+a116+a0と表すことが出来る(an,an-1, …a1,a0は0から15までの整数とする)。
ただし、偶数の場合は、2で割ることで、コラッツ操作の出発点となった整数の半分以下になる。コラッツ操作の出発点となる整数を小さい順に選択して1に収束することを証明して行けば、出発点となった整数よりも小さい整数になるということは、その整数は既に証明済みの整数ということになる。したがって、ここから奇数に絞って証明済みの整数にまで収縮することを証明する。
全ての正の奇数は、16p+1, 16p+3, 16p+5, 16p+7, 16p+9, 16p+11, 16p+13, 16p+15と表現して、これをタイプと考えることとする。つまり、全ての数をタイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15に分類し、これらについてコラッツ操作を施してみよう。
コラッツ操作を施した場合のタイプ毎の動き
この節では、16p+nを簡略化して(p, n) あるいは、<p, n>と表記することとする。ここでは、コラッツ操作を行う際の「2で割る」処理を「→」で表現している。2で割る処理が複数回続く時も、単に「→」1個で表現している場合があるので注意してほしい。
ここでは、コラッツ操作の処理途中で、最小桁が偶数の場合は、操作の途中という意味で<p, n>と表現し、最小桁が奇数となり、1回のコラッツ操作が終了した時点で(p, n)という表現を用いている。
● タイプ1
3(p, 1)+1 = <3p, 4>
pが偶数なら、<3p, 4> → <q, 2>
qが偶数なら、<q, 2> → (r, 1)
qが奇数なら、<q, 2> → <q-1, 18> → (r, 9)
pが奇数なら、<3p, 4> → <3p-1, 20> → <q, 10>
qが偶数なら、<q, 10> → (r, 5)
qが奇数なら、<q, 10> → <q-1, 26> → (r, 13)
● タイプ3
3(p, 3) + 1 = <3p, 10>
pが偶数なら、<3p, 10> → (q, 5)
pが奇数なら、<3p, 10> = <3p-1, 26> → (q, 13)
● タイプ5
3(p, 5) + 1 = <3p, 16> = <3p+1, 0> = 16(3p+1) → 3p+1
*<3p+1, 0> はタイプ別で言えば、タイプ0である。操作の途中で最小桁が0になると、<3p+1, 0> = 16(3p+1)+0 = 16(3p+1) → 8(3p+1) → 4(3p+1) → 2(3p+1) → (3p+1)となり、桁の数字が全体として、1桁小さい方にずれることになり、倍率的には<p, 5>が、<0, 3p+1>となっているので、約3/16である。ただし、(3p+1)に因数2が含まれている場合もあり、更に倍率が小さくなる可能性もある。
● タイプ7
3(p, 7) + 1 = <3p, 22>
pが偶数のとき、<3p, 22> → (q, 11)
pが奇数のとき、<3p, 22> = <3p+1, 6> → (q, 3)
● タイプ9
3(p, 9) + 1 = <3p, 28>
pが偶数のとき、<3p, 28> → <q, 14>
qが偶数のとき、<q, 14> → (r, 7)
qが奇数のとき、<q, 14> = <q-1, 30> → <r, 15>
pが奇数のとき、<3p, 28> = <3p+1, 12> → <q, 6>
qが偶数のとき、<q, 6> → (r, 3)
qが奇数のとき、<q, 6> = <q-1, 22> → (r, 11)
● タイプ11
3(p, 11) + 1 = <3p, 34>
pが偶数のとき、<3p, 34> = <3p+2, 2> → (q, 1)
pが奇数のとき、<3p, 34> = <3p+1, 18> → (q, 9)
● タイプ13
3(p, 13) + 1 = <3p, 40>
pが偶数のとき、<3p, 40> = <3p+2, 8> → <q, 4>
qが偶数のとき、<q, 4> → <r, 2>
rが偶数のとき、<r, 2> → (s, 1)
rが奇数のとき、<r, 2> = <r-1, 18> → (s, 9)
qが奇数のとき、<q, 4> = <q-1, 20> → <r, 10>
rが偶数のとき、<r, 10> → (s, 5)
rが奇数のとき、<r, 10> = <r-1, 26> → (s, 13)
pが奇数のとき、<3p, 40> = <3p+1, 24> → <q, 12>
qが偶数のとき、<q, 12> → <r, 6>
rが偶数のとき、<r, 6> → (s, 3)
rが奇数のとき、<r, 6> = <r-1, 22> → (s, 11)
qが奇数のとき、<q, 12> = <q-1, 28> → <r, 14>
rが偶数のとき、<r, 14> → (s, 7)
rが奇数のとき、<r, 14> = <r-1, 30> → (s, 15)
● タイプ15
3(p, 15) + 1 = <3p, 46>
pが偶数のとき、<3p, 46> = <3p+2, 14> → <q, 7>
pが奇数のとき、<3p, 46> = <3p+1, 30> → <q, 15>
以上の考察で、タイプ7、タイプ11、タイプ15については、コラッツ操作を1回施すことで3/2倍となり、第2桁の係数が16を超える場合があるが、このことについては別段の考慮はしていない。もし、第2桁の係数が16を超える場合は、第3桁への桁上がりを考えて<<a2+1, a1>, a0>のような記法を導入すべきかもしれないが、このことについては後で言及することとする。現時点では、タイプの遷移について思考を集中するために、第3桁への桁上がりは、無視している。なぜなら、次に示すタイプ遷移図では、最小桁と、下から2番目の桁の数が決定的に重要だからである。
タイプ遷移図
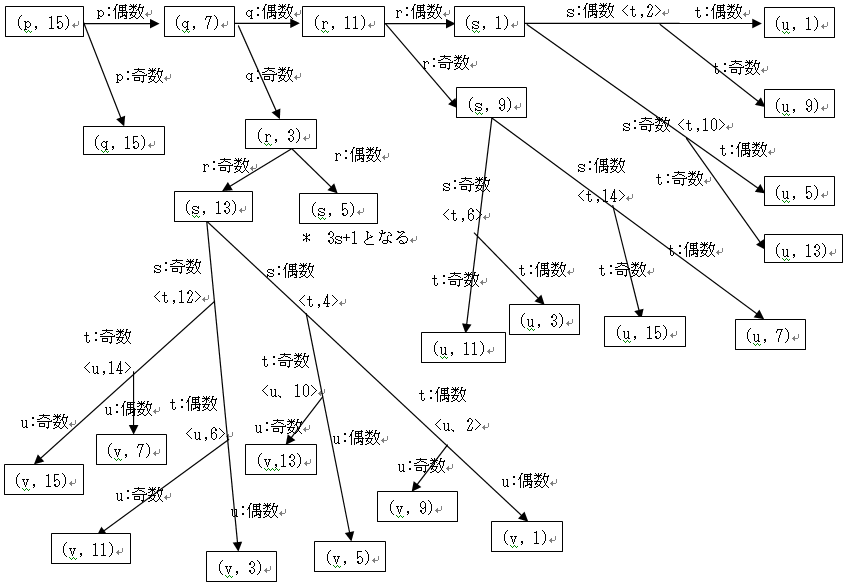
以上の考察を元にしてタイプ遷移図を描くと次のようになる。
タイプ型と、第2桁の偶数・奇数、3桁以上の整数への拡張
タイプ遷移を考えた場合に、タイプ型と第2桁の偶数・奇数が決定的に重要な働きをすることが分かった。ここまでは、2桁の整数について論じたが、議論を3桁以上の整数にまで拡張したい。
下から2番目の桁の数は「2で割る」という処理をする際の微調整の結果を反映している。最小桁が偶数で、第2桁が奇数の場合の処理については既に説明しているので、ここでは最小桁が偶数で、下から3番目の桁(第3桁)が奇数の場合について考えよう。ここで考えるのは、最小桁が偶数で、第2桁も偶数の場合である。第2桁は、最初から偶数なのか、微調整の結果、偶数になったのかはここでは問わないこととする。第3桁が奇数の場合には、第3桁を「-1」して、第2桁を「+16」するか、第3桁を「+1」して、第2桁を「-16」するかのいずれかである。「2で割る」処理が1回のタイプ3、タイプ7、タイプ11、タイプ15の場合は、「2で割る」処理によって、「+8」あるいは、「-8」という結果が残る。つまり、2桁の整数の処理の結果、第2桁が「m」だったと仮定すると、第3桁との調整を加味した場合は、「m+8」あるいは「m-8」となる。「m」の偶奇と、「m+8」あるいは「m-8」の偶奇は全く同じである。ただし、「m」の偶奇については既に2桁の整数の処理の際に解決しているものとして、ここでは問題としない。ここで、議論しているのは、第3桁からの桁下がり、あるいは第3桁への桁上がりであり、その際の第2桁の「+8」と「-8」である。
「2で割る」処理が2回必要なタイプ1とタイプ9は、最初の「2で割る」処理の際の状況は「2で割る」処理が1回の時と全く同じである。1回目の処理で桁上がりしている場合は「n-8」で、2回目の「2で割る」処理の際に桁上がりがあれば、ここに桁上がりの「-16」を加えて、それを「2で割る」ので、結果は、「n-4-8」となる。ただし、ここでも、nは、2桁のタイプ1とタイプ9の整数に対して「割る2」の処理をした時の第2桁の数字だと仮定している。従って、「-4-8」は、2桁の整数にコラッツ操作をした時と、3桁以上の整数に対してコラッツ操作をした時の差を表していることになる。同じように1回目が桁上がりか、桁下がりか、2回目が桁上がりか、桁下がりかで合わせて「n-4+8」、「n+4-8」、「n+4+8」の4通りの結果が得られる。2回目の「2で割る」処理の際に桁上がり、桁下がりがなければ、「n+4」あるいは「n-4」となる。nの偶数・奇数は、「n-4-8」、「n-4+8」、「n+4-8」、「n+4+8」、「n+4」、「n-4」と同じであることが分かる。
「2で割る」処理が3回必要なタイプ13では、第2桁は2桁の整数として3回目の処理を行った際にsだとすると、「s-2-4-8」、「s-2-4+8」、「s-2+4-8」、「s-2+4+8」、「s+2-4-8」、「s+2-4+8」、「s+2+4-8」、「s+2+4+8」の8通りとなり、あるいは、桁上がり桁下がりがない場合は、「s-2-4」、「s-2+4」、「s+2-4」、「s+2+4」となり、2回目も、3回目も桁上がり桁下がりをしていないとすれば、「s-2」、「s+2」となり、第2桁の偶数・奇数は「s」の場合と同じである。もちろん、タイプ遷移表を見ると、タイプ13は<s, 1>, <s, 9>, <s, 5>, <s, 13>, <s, 3>, <s, 11>, <s, 7>, <s, 15>に分岐し、それぞれの場合について、「s」の値は異なっているが、偶奇については変わりはない。つまり、「s」の偶奇に従って、「s-2-4-8」、「s-2-4+8」、「s-2+4-8」、「s-2+4+8」、「s+2-4-8」、「s+2-4+8」、「s+2+4-8」、「s+2+4+8」、「s-2-4」、「s-2+4」、「s+2-4」、「s+2+4」、「s-2」、「s+2」の偶奇が決まることになる。
以上の考察の結果、3桁以上の整数についても、前の節で説明したタイプ遷移図がそのまま適用できるということになる。
タイプ別の縮小と拡大の概略
コラッツ操作を行うたびに最下位桁の数値が変化していく。そして、最下位桁の数と、第2桁が偶数か奇数かによってタイプ遷移図上のコースが変化する。ここでは、タイプ遷移図上の分岐を通過する毎に出発点の整数に対してどのように増減していくかを検証し、出発点となった整数に対する倍率を示す。最下位桁の数(タイプ)を(n)で表し、タイプ(n)からタイプ(n+2)への変化を(n)(n+2)と表現することにする。
倍率が1以下になった場合はそこで出発点の整数よりも小さい整数になったものとして検証をやめる。小さい整数から順次コラッツ予想が成立することを証明するという手順で証明を進めているとすれば、出発点よりも小さな値となった時点で証明済みの整数に帰着していることになるからである。
タイプ1の整数を出発点とするとき
(1)(1): 3/4
(1)(5): 3/4
(1)(9): 3/4
(1)(13): 3/4
タイプ1の整数を出発点とする場合は、(1)か(5)か(9)、あるいは(13)に遷移する。いずれの場合も合計で3/4となり、この遷移では必ず証明済みの整数にまで収束する。
タイプ3の整数を出発点とするとき
(3)(5): 3/2 *ただし、(5)の処理の中で3/16となるので、9/32となり縮小する。
(3)(13)(1): 3/2 x 3/8 = 9/16
(3)(13)(3): 3/2 x 3/8 = 9/16
(3)(13)(5): 3/2 x 3/8 = 9/16
(3)(13)(7): 3/2 x 3/8 = 9/16
(3)(13)(9): 3/2 x 3/8 = 9/16
(3)(13)(11): 3/2 x 3/8 = 9/16
(3)(13)(13): 3/2 x 3/8 = 9/16
(3)(13)(15): 3/2 x 3/8 = 9/16
(3)を出発点とした遷移では(5)か(13)に遷移する。(5)に遷移する場合は、(5)の処理の中で、3/16され、合計として9/32となる。(3)を出発点としタイプ13に遷移する場合は、タイプ13の処理の中で3/8されるので、全体として9/16となり、必ず証明済みの整数にまで収束する。なお今後は、(n)の次に(n+2)あるいは(n+4)に分岐する時は表現を簡略化するために、”|”を使って、(n)-(n+2)|(n+4)と書くことがある。
タイプ5の整数を出発点とするとき
(5)の中の処理で3/16されるので、出発点の整数よりも小さい証明済みの整数にまで収束する。
タイプ9の整数を出発点とするとき
(9)(3): 3/4
(9)(7): 3/4
(9)(11): 3/4
(9)(15): 3/4
(9)を出発点とする場合は、このあと(3)、(7)、(11)、(15)のいずれかに遷移し、合計として3/4となり、既に証明済みの整数にまで縮小する。
タイプ13の整数を出発点とするとき
(13)(1): 3/8
(13)(3): 3/8
(13)(5): 3/8
(13)(7): 3/8
(13)(9): 3/8
(13)(11): 3/8
(13)(13): 3/8
(13)(15): 3/8
(13)を出発点とする場合は、(1)、(9)、(5)、(13)あるいは(3)、(11)、(7)、(15)に遷移する。いずれの場合も、タイプ13の処理の中で2回の分岐を行い、それによって割る2の処理を2回しているので、合計で3/2 x 1/2 x 1/2 = 3/8倍されている。従って、いずれの場合も出発点となった整数よりも小さな既に証明済みの整数にまで収束することがわかる。
タイプ7の整数を出発点とするとき
タイプ1、3、5、9、13の整数を出発点とするときは、出発点の整数よりも小さな整数に簡単に帰着することが分かったが、タイプ7、11、15の場合はどうか。タイプ7から確認してみよう。
タイプ遷移図を見ると、タイプ7の整数を出発点とするときは、タイプ3あるいはタイプ11に遷移することが分かる。
タイプ7から出発して、タイプ3を辿る場合は更にタイプ5あるいはタイプ13に遷移する。タイプ5に遷移する場合は、タイプ5の処理の中で3/16されるので、そのことを考慮すると、(7)(3)(5) = 3/2 x 3/2 x (3/16) = 27/64となる。
タイプ7から出発して、タイプ3からタイプ13に至るケースでは、タイプ13の中で3/8されることを考慮すると、次のようになる。
(7)(3)(13)(1): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(3): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(5): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(7): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(9): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(11): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(13): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(15): 3/2 x 3/2 x 3/8 = 27/32
以上のように、タイプ7からタイプ3に遷移したときはいずれの場合も、出発点の整数よりも小さい値で既に証明済みの整数に帰着することが分かる。
タイプ7から出発してタイプ11を経由する場合は、その後タイプ1か、タイプ9へと分岐する。この分岐では、タイプ7からタイプ11への遷移で、3/2となり、その後タイプ1、タイプ9への遷移で3/2となり、更にタイプ1からタイプ1、5、9、13へと遷移する。タイプ1からタイプ1、5、9、13への分岐で内部的に1/2されていることを考慮すると、3/2 x 3/2 x 3/4 = 27/16となる。
(7)(11)(1)(1): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(1)(5): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(1)(9): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(1)(13): 3/2 x 3/2 x 3/4 = 27/16
タイプ7から11を経由してタイプ9に至る場合も同様である。
(7)(11)(9)(3): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(9)(7): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(9)(11): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(9)(15): 3/2 x 3/2 x 3/4 = 27/16
これらの中で最後がタイプ1、5、9、13、3で終わっているものについては、内部処理の「割る2」があるので、減少することを簡単に証明することができるかもしれない。中でも最も簡単なのはタイプ5の場合である。タイプ5では内部処理で3/16されるので、その内部処理を考慮に入れると、(7)(11)(1)(5): 27/16 x (3/16) = 81/256となる。更に、タイプ13は内部処理で「割る2」を2回行うので、それを考慮すると、タイプ13から、次の(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への遷移で3/8されることとなるので、(7)(11)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/8 = 81/128となる。
タイプ3に分岐する場合はどうか。タイプ3では、内部処理の「割る2」がないのだが、その後タイプ5あるいはタイプ13に分岐するので大いに期待が持てる。
タイプ5に分岐する場合は次のようになる。
(7)(11)(9)(3)(5): 27/16 x 2/3 x (3/16) = 243/512となる。
タイプ3からタイプ13に分岐する場合は、次に(1)、(3)、(5)、(7)、(9)、(11)、(13)、(15)のいずれかのタイプに分岐する。3から13への分岐で、3/2され、更に13から(1)、(3)、(5)、(7)、(9)、(11)、(13)、(15)のいずれかへの分岐で3/8(= 3/2 x 1/2 x 1/2)されるので、次のようになる。
(7)(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/2 x 3/8 = 243/256
従って、いずれも出発点の整数よりも小さい既に証明済みの整数にまで収束する。
(7)(11)(1)(1)、(7)(11)(1)(9)についても、最後が内部処理で「割る2」を1回行うタイプ1とタイプ9なので少し希望が持てる。
初めに(7)(11)(1)(1)について確認する。
(7)(11)(1)(1)(1): 27/16 x 3/4 = 81/64
(7)(11)(1)(1)(5): 27/16 x 3/4 x (3/16) = 243/1024 *3/16はタイプ5の中の処理
(7)(11)(1)(1)(9): 27/16 x 3/4 = 81/64
(7)(11)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/4 x (3/8) = 243/512 *13からの先の遷移についても考慮に入れている。
(7)(11)(1)(1)(1)と、(7)(11)(1)(1)(9)についてはまだ拡張している。次に、タイプ1は、(1)|(9)|(5)|(13)に分岐し、タイプ9は(7)|(15)|(3)|(11)に分岐している。このことを考慮すると次のようになる。
(7)(11)(1)(1)(1)(1): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(1)(5): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(1)(9): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(1)(13): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
タイプ9からの分岐についても同じようになる。
(7)(11)(1)(1)(9)(3): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(9)(7): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(9)(11): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(9)(15): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
次に、(7)(11)(1)(9)についても検討する。タイプ9はその後、(7)|(15)|(3)|(11)へと分岐する。(7)、(11)、(15)は拡張してしまうが、(3)への分岐は縮小するので、(7)(11)(1)(9)(3)について検討してみよう。タイプ3はその後タイプ5あるいはタイプ13に分岐する。
タイプ5への分岐
(7)(11)(1)(9)(3)(5): 27/16 x 3/4 x 3/2 x (3/16) = 729/2048
タイプ13への分岐はその後、(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)へと分岐し、その時内部処理で3/8されるので、次のようになる。
(7)(11)(1)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/4 x 3/2 x 3/8 = 729/1024
この結果、(7)(11)(1)(9)(7)と、(7)(11)(1)(9)(11)、(7)(11)(1)(9)(15)が残ったことになる。更に、(7)(11)(9)(7)、(7)(11)(9)(11)、(7)(11)(9)(15)が残っている。(7)(11)(1)(9)(7)についてはタイプ7に戻ってしまったので、今まで計算したことがそのまま繰り返されることになる。例えば、(7)(11)(1)(9)(7)の後に収束傾向の列が続いたとしても、それが(11)(1)(1)(9)(7)の場合は、 (7)(11)(1)(1)(9)(7): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256で縮小傾向がそれほど大きくないので合計で、81/64 x 243/256 = 19683/16384となり、拡張傾向から脱却できない。(7)(11)(1)(9)(7)の後に、(11)(1)(9)(3)(13)が続くと、(7)(11)(1)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/4 x 3/2 x 3/8 = 729/1024なので、合計81/64 x 729/1024 = 59049/66176となって、出発点よりも小さな証明済みの整数以下に収束する。
タイプ11の整数を出発点とするとき
タイプ11はその後タイプ1か、タイプ9に遷移する。タイプ11から、タイプ1、タイプ9への遷移の倍率はいずれも3/2で増加する。しかし、タイプ1から(1)、(5)、(9)、(13)、タイプ9から(3)、(7)、(11)、(15)に遷移し、いずれの場合も3/2 x 1/2 = 3/4となる。従って合計で3/2 x 3/4 = 9/8となり、わずかに増加している。
(11)(1)(1): 3/2 x 3/4 = 9/8
(11)(1)(5): 3/2 x 3/4 = 9/8
(11)(1)(9): 3/2 x 3/4 = 9/8
(11)(1)(13): 3/2 x 3/4 = 9/8
(11)(9)(3): 3/2 x 3/4 = 9/8
(11)(9)(7): 3/2 x 3/4 = 9/8
(11)(9)(11): 3/2 x 3/4 = 9/8
(11)(9)(15): 3/2 x 3/4 = 9/8
タイプ11の整数が出発点の場合は、いずれもわずかに拡張している。従って、この後に、縮小傾向のタイプ1、タイプ3、タイプ5、タイプ9、タイプ13が続くときは簡単に縮小してしまうことが容易に予想される。なぜなら、タイプ1、タイプ9の場合は内部の分岐で1/2がそれぞれ1回となり、タイプ間の遷移分を合わせて3/2 x 1/2 = 3/4されるので、出発点のタイプ11からの分と合計で、9/8 x 3/4 = 27/32となるからである。タイプ13では、内部処理の分岐が2回あるので1/4となり、タイプ5ではタイプ内の処理で3/16される。また、タイプ3の場合は内部での分岐はないが、その後タイプ5あるいはタイプ13に分岐するので、それらの分を合計すると十分に1以下に収束することが予想されるからである。では実際に確認してみよう。
(11)(1)(1)(1): 9/8 x 3/4 = 27/32
(11)(1)(1)(5): 9/8 x 3/2 x (3/16) = 81/256
(11)(1)(1)(9): 9/8 x 3/4 = 27/32
(11)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 9/8 x 3/4 x 3/4 x 3/8 = 243/1024
(11)(1)(5): 3/2 x 3/4 x (3/16) = 27/128
(11)(1)(9)-(7)|(15)|(3)|(11): 9/8 x 3/4 = 27/32
(11)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 9/8 x 3/2 x 3/8 = 81/128
(11)(9)(3)(5): 9/8 x 3/2 x (3/16) = 243/512
(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 9/8 x 3/2 x 3/8 = 81/128
残ったのは(11)(9)(7): 3/2 x 3/4 = 9/8、(11)(9)(11): 3/2 x 3/4 = 9/8、(11)(9)(15): 3/2 x 3/4 = 9/8である。しかし、(11)は次に(1)あるいは(9)に分岐するので、もう少し計算してみよう。
(11)(9)(11)(1): 3/2 x 3/4 x 3/2 = 27/16
(11)(9)(11)(1)-(1)|(5)|(9)|(13): 3/2 x 3/4 x 3/2 x 3/4 = 27/16 x 3/4 = 81/64
(11)(9)(11)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/4 x 3/2 x 3/4 x 3/4 = 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(11)(9)(11)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/4 x 3/2 x 3/4 x 3/4 = 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(11)(9)(11)(1)(5): 3/2 x 3/4 x 3/2 x 3/4 x (3/16) = 27/16 x 3/4 x (3/16) = 81/64 x (3/16) = 243/1024 *(5)の内部処理も追加
(11)(9)(11)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/4 x 3/2 x 3/4 x 3/8 = 27/16 x 3/4 x 3/8 = 81/64 x 3/8 = 243/512
(11)(9)(11)は3/2 x 3/4 = 9/8なので、ここから(1)に分岐する場合は全て倍率1以下にまですんなりと収まっていることが分かる。これに対して(9)に分岐する場合はどうだろうか。計算してみよう。
(11)(9)(11)(9): 3/2 x 3/4 x 3/2 = 27/16
(11)(9)(11)(9)-(3)|(7)|(11)|(15): 3/2 x 3/4 x 3/2 x 3/4 = 27/16 x 3/4 = 81/64となり、(3)が続く時以外は拡大してしまうので、倍率1以下にまで収束するにはかなり長い道のりを必要とすることが容易に分かる。
(11)(9)(11)(9)(3)(5): 3/2 x 3/4 x 3/2 x 3/4 x 3/2 x (3/16) = 27/16 x 3/4 x 3/2 x (3/16) = 81/64 x 3/2 x (3/16) = 729/2048
(11)(9)(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/4 x 3/2 x 3/4 x 3/2 x 3/8 = 27/16 x 3/4 x 3/2 x 3/16 = 81/64 x 3/2 x 3/8 = 729/1024
残ったのは(11)(9)(7)、(11)(9)(11)(9)-(7)|(11)|(15)、(11)(9)(15)でいずれもタイプ7、タイプ11、タイプ15で終わっている。
タイプ15の整数を出発点とする時
タイプ15の整数を出発点とする場合は、それに続く遷移はタイプ7かタイプ15である。タイプ15の連続については別に考える必要があるので、ここではタイプ15からタイプ7への遷移についてのみ検討する。タイプ15からタイプ7への遷移では3/2に拡大する。タイプ7からの遷移については既に検討済みである。(7)(11)(1)(9)(7)と、(7)(11)(1)(9)(11)、(7)(11)(1)(9)(15)、(7)(11)(9)(7)、(7)(11)(9)(11)、(7)(11)(9)(15)については拡張しているので、最初にタイプ15からタイプ7への遷移で出発している場合は、更に3/2されるので、合計で拡張されることになる。(7)(11)(1)(9)(7)と、(7)(11)(1)(9)(11)、(7)(11)(1)(9)(15)、(7)(11)(9)(7)、(7)(11)(9)(11)、(7)(11)(9)(15)以外については縮小していることが分かっている。しかし、15から7に遷移する過程で既に3/2されているので、これを打ち消すほどに縮小していなくては全体として縮小しているとは言えない。つまり、タイプ15から出発した場合は、タイプ7から出発した場合と比較して、最初に3/2倍される分だけ、縮小が難しいということになる。
では実際に確認してみよう。
(15)(7)(3)(5): 3/2 x 3/2 x 3/2 x (3/16) = 81/128 *ただし、3/16はタイプ5内の処理
(15)(7)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/8 = 81/64
(15)(7)(11)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 = 81/32
(15)(7)(11)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 = 81/32
(15)(7)(3)(5)以外は全部拡大しているので、その後の分岐を検討する必要がある。
(15)(7)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)について検討する。タイプ13の次に(1)|(3)|(5)|(9)|(13)に分岐する時は減少に転じるので、出発時点の整数よりも小さい整数にまで縮小するかについて検討してみよう。簡単そうなものは、(5)|(3)|(13)の時である。
(15)(7)(3)(13)(5): 81/64 x (3/16) = 243/1024 *タイプ5の内部での処理を追加した
となり、(5)が続く時は出発点となった整数よりも小さい整数にまで帰着する。
(15)(7)(3)(13)(3)については、その後(5)|(13)が続くので、それぞれについて確認してみよう。
(15)(7)(3)(13)(3)(5): 81/64 x 3/2 x (3/16) = 729/2048
(15)(7)(3)(13)(3)(13): 81/64 x 3/2 x (3/8) = 729/1024
となり、いずれも出発点となった整数よりも小さな整数にまで収束している。(13)に更に(13)が続くときも簡単に倍率1以下に収束する。
(15)(7)(3)(13)(13): 81/64 x (3/8) = 243/512
次に(15)(7)(3)(13)-(1)|(9)について検討する。
(15)(7)(3)(13)(1)-(1)|(5)|(9)|(13): 81/64 x 3/4 = 243/256となる。(5)は更に内部処理で3/16され、(13)はその次の(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への遷移で更に3/8され、(1)|(9)では次の遷移で更に3/4されることになるが、243/256となった時点で、出発点の整数よりも小さくなっているので、ここまでで十分である。
(15)(7)(3)(13)(9)-(3)|(7)|(11)|(15): 81/64 x 3/4 = 243/256となり、いずれも出発点となった整数よりも小さい整数にまで収束している。しかし、(15)(7)(3)(13)-(7)|(11)|(15)については、いずれも拡大してしまうのでこれに続く列に関する検討は取り敢えず保留としておく。
次に、(15)(7)(11)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 = 81/32と、(15)(7)(11)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 = 81/32について検討する。(15)(7)(11)(1)-(1)|(5)|(9)|(13)については4つの場合がすべて縮小傾向であるので、一旦拡張してしまった81/32をどこまで縮小させることができるかが問題となる。
(15)(7)(11)(1)(5)については、タイプ5の中の処理で3/16される。
(15)(7)(11)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x (3/16) = 243/512
となり、一気に出発点の整数よりも小さな証明済みの整数にまで縮小する。
(15)(7)(11)(1)(13)についてもタイプ13から次の(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への遷移で3/8されるので、かろうじて出発点の整数よりも収縮することになる。
(15)(7)(11)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/8 = 243/256
(15)(7)(11)(1)(1)については、更に(1)|(5)|(9)|(13)のいずれかに分岐するが3/4なので一気に出発点の整数よりも小さくなることは難しい。同じことは、(15)(7)(11)(1)(9)についても言える。(15)(7)(11)(1)(9)はその後(7)|(15)|(3)|(11)のいずれかに分岐し、拡大率は3/4である。
(15)(7)(11)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128
(15)(7)(11)(1)(9)-(7)|(15)|(3)|(11): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128
(15)(7)(11)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128については、-(1)|(5)|(9)|(13)がいずれも縮小傾向なので、このまま処理を続けると、全体として1以下になることが期待できる。
初めに簡単そうなタイプ5、タイプ13が続く場合について確認していく。タイプ5についてはタイプ内の処理で3/16になるので、タイプ内での処理を考慮に入れると、このままで(15)(7)(11)(1)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x (3/16)= 243/128 x (3/16) = 729/2048となる。13が続く場合は、タイプ13から-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への分岐で3/8されるので、(15)(7)(11)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/8 = 243/128 x 3/8 = 729/1024となる。これに対して、タイプ1とタイプ9が続く時については、少し難しそうである。1回の延長では3/4されるだけなので、この処理を2回、3回と続ける必要がありそうである。では実際に計算してみよう。
(15)(7)(11)(1)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 = 729/512
まだだめであるが、タイプ5と13が続く時は、容易である。タイプ5が続く時はタイプ内の処理を考慮に入れるだけで問題は解決する。(15)(7)(11)(1)(1)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x (3/16)= 243/128 x 3/4 x (3/16) = 729/512 x (3/16) = 2187/8192となり出発点の整数よりも小さな証明済みの整数にまで収束する。
(15)(7)(11)(1)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/8 = 243/128 x 3/4 x 3/8 = 729/512 x 3/8 = 2187/4096となって、出発点の整数よりも小さな証明済みの整数にまで収束する。ではタイプ1とタイプ9が続く時はどうか確認してみよう。ともに3/4倍されるだけなので微妙な数字になりそうである。
(15)(7)(11)(1)(1)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 = 729/512 x 3/4 = 2187/2048となり、僅かながら倍率1以下にまでは届かない。
この場合も、タイプ5とタイプ13が続く時は簡単である。問題は、タイプ1とタイプ9が続く時である。しかし、既に2187/2048にまで辿り着いているので、更に3/4倍することで倍率1以下にまで届きそうである。ここでも、タイプ5とタイプ13が続く場合は容易である。
(15)(7)(11)(1)(1)(1)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x (3/16) = 243/128 x 3/4 x 3/4 x (3/16) = 729/512 x 3/4 x (3/16) = 2187/2048 x 3/16 = 6561/32768となり、タイプ5内の内部処理を追加しただけで、倍率1以下にまで収束した。
タイプ13については、次に-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)が続く。では計算してみよう。
(15)(7)(11)(1)(1)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/8 = 243/128 x 3/4 x 3/4 x 3/8 = 729/512 x 3/4 x 3/8 = 2187/2048 x 3/8 = 6561/16384となり、こちらも倍率1以下にまで縮小している。
さて問題のタイプ1とタイプ9の場合であるが、こちらは既に後一歩のところまで縮んでいるので、3/4で十分である。
(15)(7)(11)(1)(1)(1)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
(15)(7)(11)(1)(1)(1)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
となって、いずれも倍率1以下にまで収束している。
(15)(7)(11)(1)(1)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 = 729/512 x 3/4 = 2187/2048については、減少傾向にあるタイプ3についてだけ検証し、残りの(15)(7)(11)(1)(1)(1)(9)-(7)|(11)|(15)については保留とする。
(15)(7)(11)(1)(1)(1)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/2 x (3/16) = 243/128 x 3/4 x 3/4 x 3/2 x (3/16) = 729/512 x 3/4 x 3/2 x (3/16) = 2187/2048 x 3/2 x (3/16) = 19683/65536
(15)(7)(11)(1)(1)(1)(9)(3)(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/2 x (3/8) = 243/128 x 3/4 x 3/4 x 3/2 x (3/16) = 729/512 x 3/4 x 3/2 x (3/16) = 2187/2048 x 3/2 x (3/16) = 19683/32768
(15)(7)(11)(1)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4についてもタイプ3について検討し、(15)(7)(11)(1)(1)(9)-(7)|(11)|(15)については保留する。
(15)(7)(11)(1)(1)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/2 x (3/16) = 243/128 x 3/4 x 3/2 x (3/16) = 6561/16384となり、倍率1以下にまで収束している。
(15)(7)(11)(1)(1)(9)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/2 x (3/8) = 243/128 x 3/4 x 3/2 x (3/8) = 6561/8192となり、倍率1以下にまで収束している。
(15)(7)(11)(1)(9)-(7)|(15)|(3)|(11): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128については、タイプ3が続く場合について検証し、(15)(7)(11)(1)(9)-(7)|(15)|(11)については保留とする。
(15)(7)(11)(1)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/2 x (3/16) = 243/128 x 3/2 x (3/16) = 2187/4096となり、倍率1以下にまで収束している。
(15)(7)(11)(1)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/2 x (3/8) = 243/128 x 3/2 x (3/8) = 2187/2048となり、惜しくも倍率1以下にまでは達していない。しかし、(5)が続く時は内部処理で3/16で、(13)についてはこの後3/8、(1)|(9)については3/4、(3)についてはこの後(5)、(13)に分岐するので、倍率1以下にまで到達することになる。(15)(7)(11)(1)(9)(3)(13)-(7)|(11)|(15)のように(7)|(11)|(15)が続く時は保留とする。
(15)(7)(11)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 = 81/32についても、(15)(7)(11)(1)-(1)|(5)|(9)|(13)と同様の処理が行われることとなる。こちらは、縮小傾向のタイプ3のみを検証する。(15)(7)(11)(9)-(7)|(11)|(15)については更に拡大してしまうので、これ以降の列に関する検討は保留する。
(15)(7)(11)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x (3/16) = 81/32 x 3/2 x (3/16) = 729/1024となり、倍率が1以下にまで収束することが分った。
(15)(7)(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 = 729/512となり、倍率1以下にはまだ届いていない。(5)への分岐、(13)への分岐、(3)を経由して(5)あるいは(13)へ分岐する場合は容易であることが予想されるが、(1)と(9)についてはギリギリで届かない。-(7)|(11)|(15)はまだまだ先が遠いと考えて間違いはない。では実際に確認しよう。
(15)(7)(11)(9)(3)(13)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x (3/16) = 81/32 x 3/2 x 3/8 x (3/16) = 729/512 x (3/16) = 2187/8192
(15)(7)(11)(9)(3)(13)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/8 = 81/32 x 3/2 x 3/8 x 3/8 = 729/512 x 3/8 = 2187/4096
(15)(7)(11)(9)(3)(13)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x (3/16) = 81/32 x 3/2 x 3/8 x 3/2 x (3/16) = 729/512 x 3/2 x (3/16) = 6561/16384
(15)(7)(11)(9)(3)(13)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/2 x 3/8 = 729/512 x 3/2 x 3/8 = 6561/8192
(15)(7)(11)(9)(3)(13)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/4 = 81/32 x 3/2 x 3/8 x 3/4 = 729/512 x 3/4 = 2187/2048となってわずかに届かない。しかし、いずれも縮小列が続いているのでもうすぐである。
(15)(7)(11)(9)(3)(13)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/4 x (3/16) = 81/32 x 3/2 x 3/8 x 3/4 x (3/16) = 729/512 x 3/4 x (3/16) = 2187/2048 x (3/16) = 6561/32768 *タイプ5の内部処理を追加
(15)(7)(11)(9)(3)(13)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/4 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/8 = 729/512 x 3/4 x 3/8 = 2187/2048 x 3/8 = 6561/16384
(15)(7)(11)(9)(3)(13)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
(15)(7)(11)(9)(3)(13)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
(15)(7)(11)(9)(3)(13)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 = 729/512 x 3/4 = 2187/2048となり、こちらもわずかに届かない。こちらは(3)が続く場合だけ検証し、ー(7)|(11)|(15)が続く、(15)(7)(11)(9)(3)(13)(9)-(7)|(11)|(15)については保留として残す。
(15)(7)(11)(9)(3)(13)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x (3/16) = 81/32 x 3/2 x 3/8 x 3/4 x 3/2 x (3/16)= 729/512 x 3/4 x 3/2 x (3/16)= 2187/2048 x 3/2 x (3/16) = 19683/65536
(15)(7)(11)(9)(3)(13)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/2 x 3/8= 729/512 x 3/4 x 3/2 x 3/8= 2187/2048 x 3/2 x 3/8 = 19683/32768
(15)(7)(11)(9)(3)(13)-(7)|(11)|(15)については保留とする。
保留として残したものについての検討
今までの検討の結果、保留として残したのはタイプ7で始まる(7)(11)(1)(9)-(7)|(11)|(15)、(7)(11)(9)-(7)|(11)|(15)と、タイプ11で始まる(11)(9)-(7)|(15)と(11)(9)(11)(9)-(7)|(11)|(15)、タイプ15で始まる(15)(7)(3)(13)-(7)|(11)|(15)、(15)(7)(11)(1)(1)(1)(9)-(7)|(11)|(15)、(15)(7)(11)(1)(1)(9)-(7)|(11)|(15)、(15)(7)(11)(1)(9)(3)(13)-(7)|(15)|(11)、(15)(7)(11)(1)(9)-(7)|(15)|(11)、(15)(7)(11)(9)(3)(13)(9)-(7)|(11)|(15)、(15)(7)(11)(9)(3)(13)-(7)|(11)|(15)、(15)(7)(11)(9)-(7)|(11)|(15)と、(15)の連続である。いずれもタイプ7、タイプ11、あるいはタイプ15で始まり、タイプ7、タイプ11、タイプ15で終わっている列である。タイプ7、タイプ11、タイプ15で始まる列が全て拡大列というわけではないことは今までの検証で分かった。
保留として残したものが全体でどの程度あるかを求めてみよう。タイプ1、3、5、9、13で出発した列は全て倍率1以下にまで収束することが分った。つまり、5/8は直ちに収束する。これに対して、タイプ7、タイプ11、タイプ15から出発した整数列は直ちに収束するとは限らないことが分かった。3/8のうちどの程度が拡散列として残るのか計算してみよう。
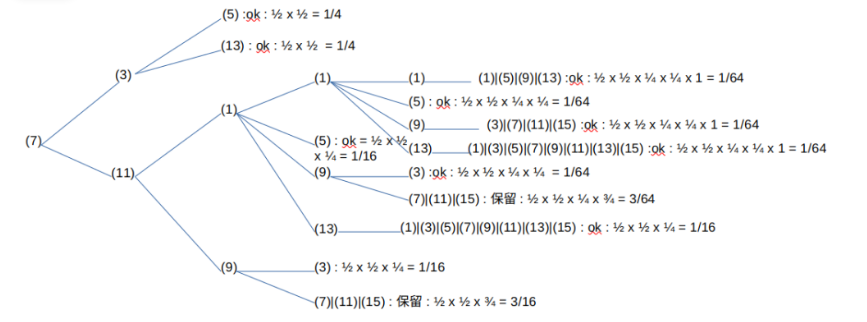
枝葉の最後に示したのは、縮小するか拡大列として保留するか、その場合の出現割合である。縮小して倍率1以下にまでなる場合は”ok”と、拡大列として保留する場合は”保留”と表示した。
上の図のように倍率1以下に確実に収縮することを示せたのは1/4 + 1/4 + (1/64) x 4 + 1/16 + 1/64 + 1/16 + 1/16 = 49/64で、最初にタイプ7が選ばれるのは、1/8なので、それを合わせると1/8 x 49/64 = 49/512ということになる。拡大基調にあるとして保留としたのは15/64で、最初にタイプ7が選択される場合の1/8を考慮に入れると、15/512となる。
次に最初に11が来る場合について考えてみよう。
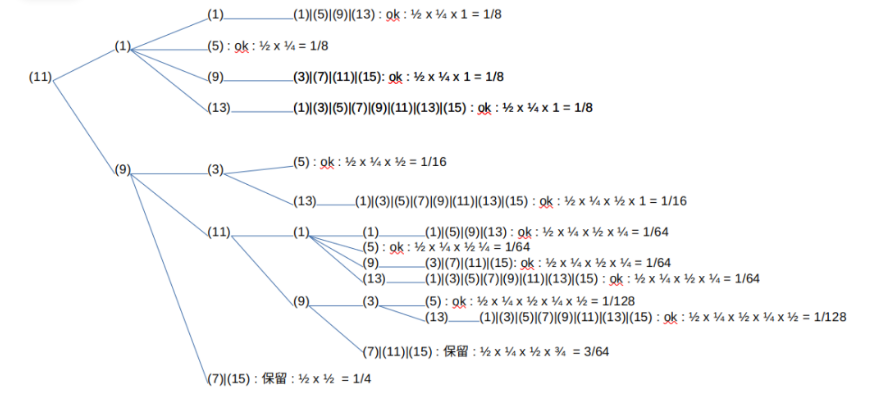
拡大基調だとして保留したのは3/64と1/4で合わせると、19/64となる。最初に11が来るのは1/8なので、合計すると1/8 x 19/64 = 19/512ということになる。
次にタイプ15から開始される場合について計算してみよう。
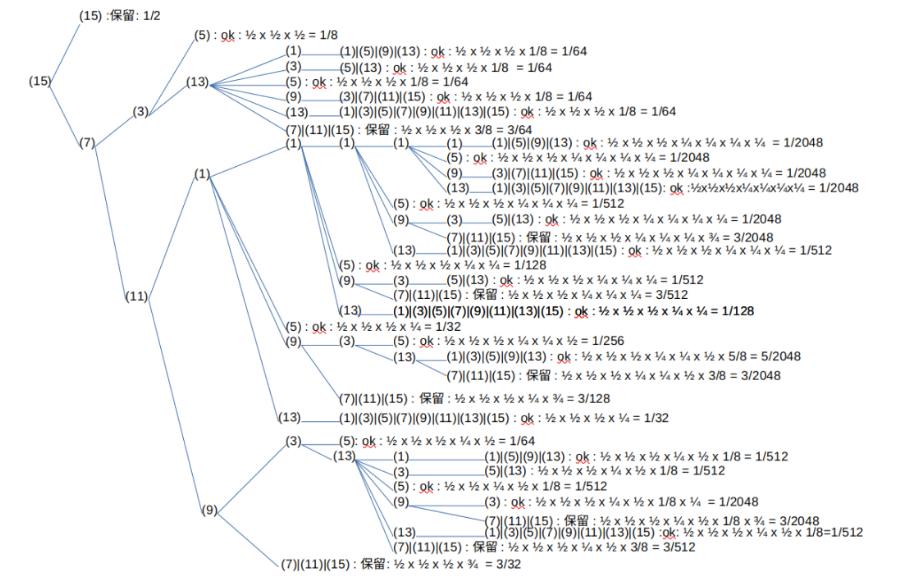
タイプ7の前にタイプ15が追加されているだけなのにタイプ7の図と比較すると格段に複雑になっていることがすぐに分かる。タイプ15が先頭に来ることで最初に3/2倍されることになる。従って、その後に縮小列が続くとしても、必ずしも最初の3/2の影響を払拭することができないため、タイプ7が最初に来る場合と比較して難しくなるためである。
では、タイプ15が先頭に来る場合の計算をしてみよう。初めに、(7)|(15)に分岐する。ここでは、(15)のループについては考慮しない。何故なら、タイプ15のループは必ずタイプ7に変容するからである。このことについては後で証明する。従って、ここではタイプ15からタイプ7への分岐だけ考えることにして、(15)のループは保留の計算にも合算しない。保留となる場合を足していくと、3/64 + 3/2048 + 3/512 + 3/2048 + 3/128 + 3/2048 + 3/512 + 3/32 = 269/2048となり、最初にタイプ15が来る割合は1/8なので、全体として269/16384となる。
タイプ7から出発したときの保留の率は15/512、タイプ11から出発したときの保留の率は19/512、タイプ15から出発したときの保留の率は269/16384となる。これらを平均すると(15/512 + 19/512 + 269/16384)/3 = ((480 + 608 + 269)/16384)/3 = (1357/16384)/3 = 0.082824707/3 = 0.027608236 ≒ 1/40
以上の計算結果を踏まえるて、保留として残したタイプ列に更にコラッツ操作を追加するとどうなるか考えてみよう。最初にタイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15のいずれかの整数で出発する。それぞれの割合は1/8ずつである。そして、タイプ1、タイプ3、タイプ5、タイプ9、タイプ13で出発した整数は全て出発点の整数よりも小さな整数にまで収束し、その時点で証明済みの整数にまで縮んだことになる。割合としては、5/8である。これに対して、タイプ7で出発した整数は、15/64が出発点の整数にまで縮まりきらない。タイプ7で出発する割合と合わせると15/512が出発点の整数よりも拡大してしまうことになる。タイプ11で出発した整数は、19/64が拡大してしまう。タイプ11で始まる割合の1/8と合わせると、19/512ということになる。タイプ15は拡大の割合が極めて高い。それはタイプ15からタイプ15へと戻ってしまう割合が1/2あるからである。この(15)から(15)へのループについては別途証明することにして分けて考えることにする。そうすると、総合で269/2048あり、更にタイプ15で出発する割合である1/8を掛け合わせると269/16384となる。1
タイプ7、タイプ11、タイプ15で始まる場合で拡大基調で終わっている場合は、全てタイプ7、タイプ11、タイプ15で終わっている。これらについて更にコラッツ操作を継続すると最初の計算とは少し違ってくる。最初はタイプ7、タイプ11、タイプ15で始まる割合はそれぞれ1/8ずつということになるが、その後のタイプ7、タイプ11、タイプ15で保留した後の計算では、この1/8は計算に入らない。従って、拡大基調の割合は、(15/64 + 19/64 + 269/2048)/3 = ((480 + 608 + 269)/2048)/3 = 0.220865885 ≒ 1/5となる。
最初の計算では全体として39/40は減少傾向で、1/40は更に拡大するという結果が得られたが、次はこの1/40に対してはタイプ7、タイプ11、タイプ15に対するコラッツ操作のみが継続されるからである。
タイプ7からは(3)あるいは(11)に分岐して、(3)は縮小傾向である。タイプ11からは(1)あるいは(9)に分岐していずれも縮小傾向である。これに対してタイプ15は(7)あるいは(15)に分岐していずれも拡大傾向である。

拡大傾向の列に後続の列を続けてみると次のようになる。
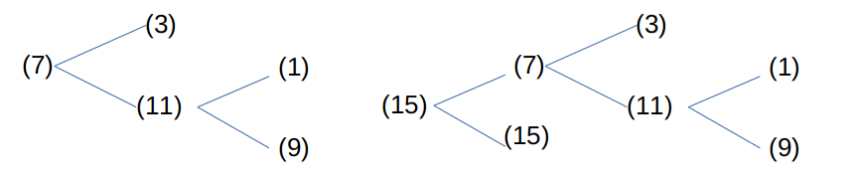
(15)が連続する場合以外は、減少傾向の列が続くことになる。もちろん、減少傾向の列が続いても直ちに倍率1以下になるとは言えない。一旦拡大してしまっているので、単純な計算はできないからである。例えば、(7)で終わっている列に続いて、(11)(9)と続くと縮小するが、(9)の後に更に-(7)|(11)|(15)が続いてしまうとまた拡大してしまうし、(11)(9)-(3)と続いたとしても倍率1以下にまで縮小するとは断言できない。例えば、(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)と分岐する時は大抵の場合はここで倍率1以下になるのだが、運悪くそうならない場合は(11)(9)(3)(13)-(7)|(11)|(15)からまた拡大傾向に転じてしまう可能性がある。つまり、拡大傾向の列に後続の列が続いている場合、それが縮小傾向の列だとしても、今までの列の倍率を打ち消して倍率1以下にまで持っていけるかどうかが重要となってくる。ただ確実に言えることは、どんな列が続いたとしても、それが(15)でなければ倍率1以下にまで行く列が確実に増えていくことである。更に、有限の整数を扱う限り、(15)の連続はやがて止まり、(7)タイプに変化することである。そして、(7)タイプに変化すると、そこから確実に減少傾向になる列が現れて倍率1以下になっていく列の数が確実に増えていくことである。
第2桁の偶数・奇数の割合
保留として一旦計算を止めていたところから再度計算を始める際の、(7)、(11)、(15)への分岐について、その際の第2桁の偶数奇数について考えてみたい。偶数になるか奇数になるかの割合が同じなら拡大傾向からの計算の割合を、縮小は4/5、拡大率は1/5と単純に計算できるからである。
初めに、第3桁を「0」として、第2桁との組み合わせを考えることにする。忘れてはいけないのは、第1桁からの桁上がりである。桁上がりするのは第1桁が、5~15(の奇数)の場合で、桁上がりしないのは1と3である。従って、桁上がりするのは6/8、桁上がりしないのは2/8ということになる。
3<0, 1> = <0, 3>で、第1桁からの桁上がりがない場合は、2で割るために第2桁を-1することになり(その結果、第1桁は+16されることになる)<0, 2>となり、桁上がりがある場合は<0, 4>となる。これらをそれぞれ2で割るので、<0, 2> → <0, 1>、<0, 4> →<0, 2>となる。つまり、<0, 1>となるのが1/4で、残りの3/4は<0, 2>となる。
3<0, 2> = <0, 6>で、第1桁は(3n+1)/2の処理の結果、必ず偶数になっているはずなので、単純に2で割って、<0, 3>となる。
以下同様に計算をすると、次のようになる。
3<0, 3> = <0, 9>で、第1桁からの桁上がりのない1/4の場合は、<0, 8/2> = <0, 4>。第1桁からの桁上がりのある3/4の場合は、<0, 10/2> = <0, 5>
3<0, 4> = <0, 12> → <0, 6>
3<0, 5> = <0, 15>で、第1桁からの桁上がりのない1/4の場合は、<0, 14/2> = <0, 7>。第1桁からの桁上がりがある3/4の時には、<0, 16/2> = <0, 8>
3<0, 6> = <0, 18> → <0, 9>
3<0, 7> = <0, 21>で、第1桁からの桁上がりのない1/4の場合は、<0, 20/2> = <0, 10>。第1桁からの桁上がりがある3/4の時は、<0, 22/2> = <0, 11>
3<0, 8> = <0, 24> → <0, 12>
3<0, 9> = <0, 27>で、第1桁からの桁上がりのない1/4の場合は、<0, 26/2> = <0, 13>。第1桁からの桁上がりのある時は、<0, 28/2> = <0, 14>
3<0, 10> = <0, 30> → <0, 15>
3<0, 11> = <0, 33>で、第1桁からの桁上がりのない1/4の場合は、<0, 32/2> = <0, 16> = <1, 0>。第1桁からの桁上がりのある時は、<0, 34/2> = <0, 17> = <1, 1>
3<0, 12> = <0, 36> → <0, 18>
3<0, 13> = <0, 39>で、第1桁からの桁上がりのない1/4の場合は、<0, 38/2> = <0, 19> = <1, 3>。第1桁からの桁上がりのある時は、<0, 40/2> = <0, 20> = <1, 4>
3<0, 14> = <0, 42> → <0, 21>
3<0, 15> = <0, 45>で、第1桁からの桁上がりのない1/4の場合は、<0, 44/2> = <0, 22> = <1, 6>。第1桁からの桁上がりのある時は、<0, 46/2> = <0, 23> = <1, 7>
第2桁が偶数の場合は、操作の結果、交互に奇数、偶数が現れる。つまり、奇数、偶数の出現割合は全く同じである。第2桁が奇数の場合は、<0, 1>、<0, 5>、<0, 9>、<0, 13>の場合は、奇数が1/4で、偶数が3/4。<0, 3>、<0, 7>、<0, 11>、<0, 15>の場合は逆に偶数が1/4で、奇数の出現割合が3/4となり、こちらも総合的には奇数と偶数が全く同じ割合で出現することが分かった。
(7)、(11)、(15)の場合も常にこのタイプが続くわけではない。途中で(1)、(5)、(9)、(13)が続くこともある。この場合は、このタイプの中で割る2の処理が加わることになる。(1)、(9)では1回、(13)では2回、(5)の場合は最低でも4回加えられる。また、(3)の場合は、(5)や(13)を経由することで内部処理が加えられることになる。このタイプ内の処理ではただ単に2で割るだけである。その前提として、第1桁は0~14の偶数になっていることである。単に2で割るだけなので、第1桁からの桁上がりはない。しかし、第2桁が奇数の場合は、第2桁を-1して、第1桁を+16する処理が必要となる。では、<第3桁、第2桁>について「割る2」の処理を計算してみよう。
<0, 0> → <0, 0>
<0, 1> → <0, 0>
<0, 2> → <0, 1>
<0, 3> → <0, 1>
<0, 4> → <0, 2>
<0, 5> → <0, 2>
<0, 6> → <0, 3>
<0, 7> → <0, 3>
<0, 8> → <0, 4>
<0, 9> → <0, 4>
<0, 10> → <0, 5>
<0, 11> → <0, 5>
<0, 12> → <0,6>
<0,13> → <0, 6>
<0, 14> → <0, 7>
<0, 15> → <0, 7>
16通りのうち、第2桁が偶数になるのが8通りで、第2桁が奇数になるのは8通りとなり、全く同じ割合になる。
(3n+1)/2の処理と、単に「/2」(割る2)の処理のいずれでも、第2桁が偶数になるのか奇数になるのかの割合が全く同じである事が分かった。
桁を増やしてみよう
ここまで、<第3桁、第2桁>で、(3n+1)/2の処理では、第1桁は0~15の奇数、「割る2」(/2)の処理では、第1桁は0~14の偶数という形で考えてきた。そして、第3桁は計算の最初は「0」である。今度は、第3桁が1~15の場合について考えてみよう。この場合には、(3n+1)/2あるいは、「/2」の処理をする際に、第3桁と第2桁の調整が必要となってくる。調整は最初に第1桁と第2桁の間で、次に第2桁と第3桁の間で行うものとしよう。すでに、第1桁と第2桁の調整は済んでいて共に偶数となっているものとする。(3n+1)/2の処理では、第1桁は最初は0~46、第2桁、第3桁は最初は、0~45の間の値になっているはずであるが、桁の数が「16~31」の時は元の桁を-16して、上の桁に+1桁上がりさせる。桁の数が「32~45(あるいは46)」の場合は元の桁を-32して、上の桁に+2桁上がりさせていて、既に、各桁の値は全て「0~15」の数字になっているものとしよう。この調整の際には、下の桁の偶数・奇数の割合に変化がない。なぜなら、±16、あるいは±32されるだけだからである。
第3桁が偶数ならそのまま2で割ればよいが、第3桁が奇数の場合は問題となる。第3桁が奇数なら、第2桁を+16して、第3桁を-1する処理が必要であり、その上で2で割ると、第2桁が偶数になるか奇数になるかの割合は全く同じである。なぜならば、第2桁は+16されるだけで、2で割る処理をしたときの偶数奇数に全く影響しないからである。従って、計算結果の偶数奇数の割合は全く同じという結論は上で計算した場合と全く同じことになる。
(1)、(9)が続く時は「/2」の処理が1回加わる。この場合は、第1桁は既に偶数となっているはずであるので、第1桁と第2桁の調整で第2桁を偶数にする。そして、第3桁が奇数なら、第2桁を+16して、第3桁を-1することになる。(13)の場合は2で割る処理がさらに1回追加される。この場合は、先程の第2桁の+16は1回目の割る2の処理の結果+8となり、新しい処理の結果が加わる。もし、第2回目の割る2の処理の前に、第3桁が奇数なら+16が加わることになり、2で割ると+8+4となる。(5)への分岐の場合は更に2で割る処理がもう1回追加され、それぞれの内部処理で第3桁が奇数の場合、偶数の場合を全て考慮に入れると、+8+4+2、+8+2、+8+4、+8、+4+2、+4、+2などとなる。いずれの場合も、第2桁の偶数・奇数に影響を与えない。ただ、各処理の間で各桁の間に調整が加わっていると考えれば、第1回目の内部処理と、第2回目の内部処理を別にして考える必要はない。
(3n+1)/2と/2の処理で偶数奇数はどうなるのか
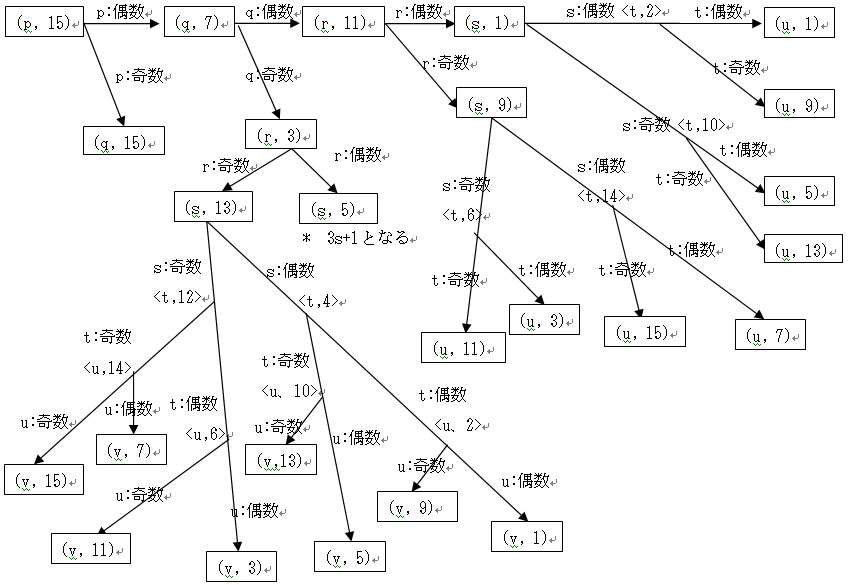
(3n+1)/2と「/2」の処理で各桁の数字がどのように変化するか見てみよう。ただし、ここでは第2桁以上の桁について考えているので、(3n+1)/2の処理では、実際には3n/2で計算している。3n/2は青色の矢印で表し、「/2」の処理は赤色の矢印で表した。偶数は2通りに分かれるがそのうち0、4、8、12は2つとも偶数になり、2、6、10、14は2つとも奇数となる。奇数は3つの場合に分かれるが、この内、1、5、9、13は2/3が偶数、1/3が奇数となる。これに対して、3、7、11、15は2/3が奇数、1/3が偶数となる。従って、偶数の場合も、奇数の場合も、3n/2と「/2」の処理で各桁の数字が偶数になるか、奇数になるかの割合は全く同じである。
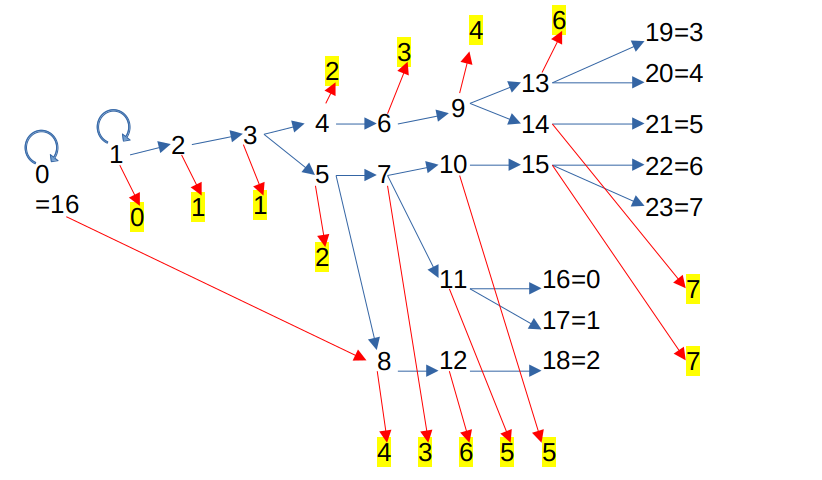
タイプ遷移図を確認すると、全ての分岐は第2桁が偶数か奇数かによっていることが分かる。例えば、今第2桁が1だったと仮定してみよう。コラッツ操作の(3n+1)/2の処理(実際は2桁以上は3n/2)、「/2」の処理をするたびに第2桁は変化して行くが、その変化は上の樹形図のようになる。常に偶数・奇数が同じ割合で変化していくわけではないが、総合的に見ると、第2桁が偶数での分岐と、第2桁が奇数での分岐は全く同じ割合で発生していることになる。
これは、4桁の整数、5桁の整数、6桁の整数でも全く同じである。3n/2と「/2」の処理では、各桁の数字を小さい桁から順に2桁ずつ調整をして、桁を偶数に変えていく処理をして2で割るだけである。既に見てきたようにこの処理をすることによって第2桁が偶数になるのか奇数になるのかは全く同じ割合である。
直下の桁との調整については以上であるが、今度は上の桁との調整について考えてみよう。全ての桁が0~15に調整され、更に下位桁から順次偶数に調整できたと仮定しよう。この段階で、当該桁の上の桁が奇数の場合、上の桁が-1され、当該桁は+16されることになる。その後、「割る2」の処理が1回行われると、+16は+8となる。タイプ1と9では、更に「割る2」の処理が1回加わる。この時、上の桁が偶数なら、+4となり、奇数なら+8+4となる。タイプ13の場合は、更に「割る2」の処理が加えられることになる。その結果当該桁の変化は、+8+4+2、+8+2、+4+2、+2のいずれかとなる。いずれの場合も当該桁の偶数奇数には変化がないことになる。
では、(3n/2)(/2)、あるいは(3n/2)(/2)(/2)の処理の後に更に(3n/2)が加わった時はどうか検証してみよう。次に示すのは、(3n/2)(/2)の場合である。
3(+8+4)/2 = 36/2 = 18 → 18-16=5
3(+8)/2 = 24/2 = 12
3(+4)/2 = 12/2 = 6
いずれも桁下がり分は偶数のままなので、元の桁の偶数・奇数には影響はない。
次は、(3n/2)(/2)(/2)の場合である。
3(+8+4+2)/2 = 42/2 = 21 → 21-16=5
3(+8+2)/2 = 30/2 = 15
3(+4+2)/2 = 18/2 = 9
3(+2)/2 = 6/2 = 3
となる。いずれの場合にも、桁下がりした分が奇数になるので、当該桁の偶数奇数が入れ替わることになる。しかし、これは入れ替わるだけなので、偶数になる割合と奇数になる割合が同じということはこれまでと同じである。
拡張列を更に追跡すると
既に示したようにタイプ7を起点としてコラッツ操作を施した場合は15/512が拡張傾向として保留とされた。最初の1/8を取り去ると、縮小と拡大の割合は49/64 : 15/64 = 49 : 15である。タイプ11を起点とした時の保留率は19/512である。最初の1/8を取り除くと、縮小と拡大の割合は45/64 : 19/64 = 45 : 19となる。
タイプ15はやがてタイプ7になることが分かっているので(このことについてはこの後証明する)、タイプ15からタイプ7を経て保留となる率を考えてみる。これは、1393/2048からいきなり15タイプが連続する率の1/2を引けばいいので、1393/2048 – 1/2 = (1393-1024)/2048 = 369/2048となる。縮小と拡大の割合は1679 : 369 = 4.550135501 : 1 ≒ 9 : 2となる。
タイプ11は第2桁の数が偶数の時はタイプ1となり、奇数の場合はタイプ9となり、この後は縮小傾向となり、その後は拡大縮小を続けながらも全体的には小さな整数になっていく。タイプ11を起点とした時の保留率は19/64であり、45/64は倍率1以下にまで収束してしまう。では、一旦保留したところを起点として次の操作を始めるとどうなるか。一旦保留したところから再度処理を開始すると、そこではタイプ7、あるいはタイプ11、タイプ15からの再出発となる。この時の縮小の割合は4/5で拡張の割合は1/5である。そして縮小傾向からの再出発ではやはり縮小割合は45/64、拡張割合は19/64となり、再度タイプ7、タイプ11、タイプ15から開始する場合は縮小割合は4/5、拡張割合は1/5として再出発することになる。以下この繰り返しである。これを図解すると次のようになる。
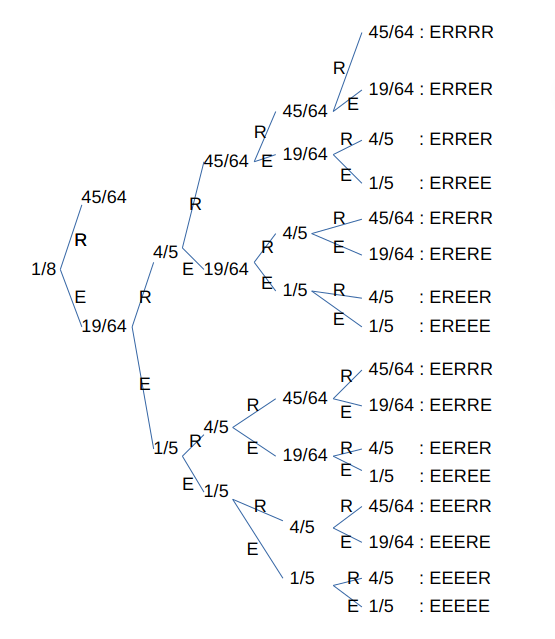
数回のコラッツ処理で、タイプ7、タイプ11、タイプ15に到達して、もう一度コラッツ処理をやり直すまでを、「一連のコラッツ処理」と呼ぶことにする。最初の「一連のコラッツ処理」で縮小した45/64は倍率1以下にまで縮小している。従って、2回めの「一連のコラッツ処理」では、拡張してタイプ7、タイプ11、タイプ15に到達して保留となった処理列のみ計算を継続している。一旦保留で計算を停止した箇所からの再スタートはタイプ7、タイプ11、タイプ15を起点とする計算となるので、縮小率は4/5、拡大率は1/5となる。そして縮小傾向の列については、倍率1以下にまで到達してしまっているものもあるはずであるが、今はそのことは計算に入れていない。そして、縮小傾向からの再出発は通常の再出発(つまり、タイプ7、タイプ11、タイプ15に到達してしまったとして停止させたところからの再出発ではなく)となるので、縮小率は45/64、拡大率は19/64となる。
問題は縮小傾向の列(一連のコラッツ処理)と拡張傾向の列(タイプ7、タイプ11、タイプ15に達して一旦停止させたもの)の回数が同じ場合を、全体として縮小とするかどうかだ。1回のコラッツ操作なら拡張は3/2、縮小は4/3と評価できるが、今ここで考えているのは保留と判断するまでの一連のコラッツ処理の連続である。これをタイプ11で見てみよう。タイプ11で保留として残したのは(11)-(9)-(7)|(15)と、(11)-(9)-(11)-(9)-(7)|(11)|(15)の2通りの場合である。(11)-(9)-(7)|(15)の倍率は3/2 x 3/4 = 9/8、(11)-(9)-(11)-(9)-(7)|(11)|(15)の倍率は3/2 x 3/4 x 3/2 x 3/4 = 81/64である。縮小の割合はどうか。縮小率は最初の起点である(11)から(11)-(1)|(9)の分岐での3/2を倍率1以下に縮小させているので2/3と考えて良い。そうすると9/8 x 2/3 = 18/24、81/64 x 2/3 = 162/192となり、いずれも倍率は1以下になっている。以上のことを考えると、拡張と縮小の回数が同じREとERの場合は縮小しているということができる。
以上の考察を元にして縮小の率を計算してみることとする。
1回目の一連のコラッツ処理の終了時点:
縮小率:45/64 = 0.703125
拡大率:19/64
2回目の一連のコラッツ処理の終了時点:
縮小率:45/64 + 19/64 x 4/5 = 0.703125 + 0.2375 = 0.940625
3回目の一連のコラッツ処理の終了時点:
縮小率:45/64 + 19/64 x 4/5 x 45/64 = 0.870117
4回目の一連のコラッツ処理の終了時点:
縮小率:45/64 + (19/64 x 4/5 x 45/64 x 45/64 + 19/64 x 4/5 x 45/64 x 19/64) + 19/64 x 4/5 x 19/64 x 4/5 + 19/64 x 1/5 x 4/5 x 45/64 = 45/64 + 19/64 x 4/5 x 45/64 + 19/64 x 4/5 x 19/64 x 4/5 + 19/64 x 1/5 x 4/5 x 45/64 = 0.870117 + 19 x 4(74 + 45)/(64x5x64x5) = 0.870117 + 0.089805 = 0.959922
5回めの一連のコラッツ処理の終了時点:
縮小率:45/64 + (19/64 x 4/5 x 45/64 x 45/64 x 45/64 + 19/64 x 4/5 x 45/64 x 45/64 x 19/64) + 19/64 x 4/5 x 45/64 x 19/64 x 4/5 + 19/64 x 4/5 x 19/64 x 4/5 x 45/64 + 19/64 x 1/5 x 4/5 x 45/64 x 45/64 = 45/64 + 19/64 x 4/5 x 45/64 x 45/64 + 19/64 x 4/5 x 45/64 x 19/64 x 4/5 + 19/64 x 4/5 x 19/64 x 4/5 x 45/64 + 19/64 x 1/5 x 4/5 x 45/64 x 45/64 = 0.703125 + 19x4x452/643x5 + (42x192x45 + 42x192x45 + 4x19x452)/52x643 = 0.703125 + 0.123097 + 0.102804 = 0.929026
第2回目から第3回目のところで縮小率が若干下がっているが、これは縮小と拡大が同じ回数の時の扱いが原因で、縮小と割合の回数が同じ場合が現れる偶数回目の場合は、奇数回目に比較して縮小の率が上がるためである。偶数回目、奇数回目という捉え方をすると一連のコラッツ処理が増えるに従って徐々に縮小の率が増えている。更に、縮小列の中には、そのまま倍率1以下になってそれ以降の計算が必要ないものも含まれていくので、実際の縮小の割合はこの計算よりも更に増えていくことになる。
タイプ7の場合も同様に考えることができる。第1回目の「一連のコラッツ処理」の結果、倍率1以下にまで縮小するのは15/64で、拡張傾向として計算を途中でやめて保留としたのが49/64である。そして、保留分に対して再計算をスタートする場合は、そこからはタイプ7、あるいはタイプ11、タイプ15を起点とした再スタートとなる。この時の収縮率は4/5で拡張率は1/5となる。
タイプ7の場合に保留として残したのは(7)-(11)-(1)-(9)-(7)|(11)|(15)と、(7)-(11)-(9)-(7)|(11)|(15)の2通りである。(7)-(11)-(1)-(9)-(7)|(11)|(15)の場合の倍率は3/2 x 3/2 x 3/4 x 3/4 = 81/64で、(7)-(11)-(9)-(7)|(11)|(15)の場合の倍率は3/2 x 3/2 x 3/4 = 27/16となる。縮小と拡大が同じ回数の場合は81/64 x 2/3 = 162/192、27/16 x 2/3 = 54/48となる。出現率は162/192が3/64で、54/48が3/16である。出現率を加味すると、倍率は(162/192 x 1/5 + 54/48 x 4/5) = 1026/960で僅かに拡張していることになる。従って、タイプ7を起点とする場合は、縮小列と拡大列が同数の場合は、拡張として場合分けすることにする。以上の考察を元に縮小率を計算すると次のようになる。
1回目の一連のコラッツ処理の終了時点:
縮小率:49/64 = 0.765625
拡大率:15/64
2回目の一連のコラッツ処理の終了時点:
縮小率:49/64 = 0.765625
3回目の一連のコラッツ処理の終了時点:
縮小率:49/64 + 15/64 x 4/5 x 49/64 = 0.765625 + 0.143554 = 0.909180
4回目の一連のコラッツ処理の終了時点:
縮小率:49/64 + 15/64 x 4/5 x 49/64 x 49/64 = 0.765625 + 0.109909 = 0.875534
5回目の一連のコラッツ処理の終了時点:
縮小率:49/64 + (15/64 x 4/5 x 49/64 x 49/64 x 49/64 + 15/64 x 4/5 x 49/64 x 49/64 x 15/64) + 15/64 x 4/5 x 49/64 x 15/64 x 4/5 + 15/64 x 4/5 x 15/64 x 4/5 x 49/64 + 15/64 x 1/5 x 4/5 x 49/64 x 49/64 = 49/64 + 15/64 x 4/5 x 49/64 x 49/64 + 15/64 x 4/5 x 49/64 x 15/64 x 4/5 + 15/64 x 4/5 x 15/64 x 4/5 x 49/64 + 15/64 x 1/5 x 4/5 x 49/64 x 49/64 = 0.765625 + 0.109909 + (42x152x49 + 42x 152x49 + 4x15x492)/(52x643) = 0.765625 + 0.109909 + 0.04217 = 0.917703
タイプ7の場合も縮小率は揺らぎながら徐々に増加していることが分かる。タイプ7の場合は、縮小の列と拡大の列の個数が同じ場合は拡大として扱ったので、偶数回目の縮小率が落ちている。しかし、偶数回だけ、あるいは奇数回だけを見ると、一連のコラッツ処理の回数が増えるごとに縮小率が少しずつ上がっていることが分かる。また、このことはタイプ11の時にも述べたが縮小列が倍率1以下にまで収束すれば、そこで証明終わりと判断して、それ以降の計算の対象とはならないので、実際は上の計算結果よりも縮小率は高くなる。
タイプ15についても全く同じことが言える。縮小列と拡大列の出現回数が同じ場合を縮小と判断しても、拡大と判断しても全体的には縮小率が一連のコラッツ処理をすればするほど縮小率が上がっていくので、タイプ15についても同じことが言える。
タイプ7、タイプ11のモデル化
<只今修正中です。><2026/01/27>
ここまでの計算では、より正確を期すため縮小列からの縮小・拡大と、拡大列として一旦保留した時の再計算での縮小・拡大を分けて考えたため、計算が複雑になってしまった。ここでは、縮小列における縮小・拡大と拡大列として一旦保留した時点から再出発する際の縮小・拡大を同じにして計算してみよう。タイプ7、タイプ11、タイプ15を出発点とした時の拡大率は平均で1/5なので、縮小率は4/5となる。これを元にして計算してみよう。
一連のコラッツ操作を6回施した後の縮小率の合計は次のようになる。
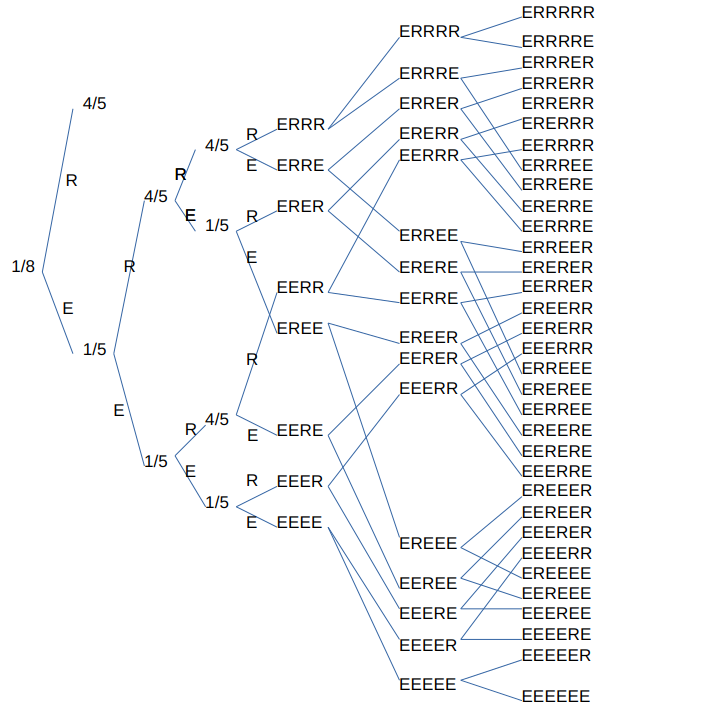
n = 1 のとき
4/5
n = 2のとき
4/5 +(1/5)x (4/5)
n ≧ 3で、n/2 = 整数の時(ただし、r≦(n+1)/2)
4/5 +(1/5)x (4/5)n-1 + n-1C1(4/5)n-2(1/5) + …… + n-1Cr(4/5)n-r-1(1/5)r
n≧3で、(n-1)/2 = 整数の時(ただし、r<(n-1)/2)
4/5 + (1/5)x(4/5)n-1 + n-1C1(4/5)n-2(1/5) + …… + n-1Cr(4/5)n-r-1(1/5)r
「一連のコラッツ処理」の4回目を見てみよう。ここで一連のコラッツ操作での処理の結果得られた列のうち、縮小と拡大の個数が同じ場合は縮小するとみなすこととする。縮小率で言うと、縮小3回縮小1回のERRR、縮小2回拡大2回のERRE、ERER、EERR、縮小1回拡大3回のEREE、EERE、EEER、縮小0回拡大4回のEEEEに分けることができる。ここで、ERRRをAで表し、その縮小率をa、ERRE、ERER、EERRをそれぞれB、C、Dと表し縮小率をそれぞれb、c、dとするものとする。更に、EREE、EERE、EEERをそれぞれE、F、Gとして、その時の縮小率をそれぞれe、f、gとする。この時縮小率の合計は4/5 + a + b + c + dということになる。5回目は、縮小列と拡大列が同数ということはない。従って、縮小3回拡大2回は縮小、縮小2回拡大3回は拡大ということになる。従って、5回目の縮小率の合計は4/5 + a x 4/5 + a x 1/5 + (b + c + d) x 4/5 = 4/5 + a + (b + c + d) x 4/5となり、(b + c + d) x 1/5分だけ減少していることになる。6回目は縮小と拡大が同じ回数出現する場合は縮小と考えるので、縮小率の合計は次のようになる。4/5 + a x 4/5 + a x 1/5 + (b + c + d) x (4/5)2 + (b + c + d) x 4/5 x 1/5 + (b + c + d) x 1/5 x 4/5 + (e + f + g) x (4/5)2=4/5 + a + (b + c + d) x 4/5 + (e + f + g) x 16/25となり、第5回と比較すると、(e + f + g) x 16/25だけ縮小率が増加していることになる。b、c、dはそれぞれ(4/5)2 x (1/5)2で、e、f、gはそれぞれ(4/5) x (1/5)3なので、(b + c + d) : (e + f + g) = 4 : 1 となる。従って、(a + b + c) x 1/5 : (e + f + g) x 16/25 = 4/5 : 16/25 = 5 : 4となる。従って、縮小率は4/5 + aで、aは1/5 x 4/5 = 4/25なので、偶数回目と奇数回目で増減を繰り返すが、その波の振幅は徐々に小さくなり、最終的に24/25に近づいていくことになる。同じことが、第(2m)回目、第(2m+1)回目、第(2m+2)回目の間にも言える。また、縮小列と拡張列の回数が同数の場合は拡張とみなすと、波の位相が180度ずれることになる。そして、縮小列のうちのいくつかは「一連のコラッツ処理」の間に倍率1以下にまで到達するのでその率をαで表すと、縮小率は24/25 + αとなり、「一連のコラッツ処理」を重ねるごとにαはどんどん増大していくことになるので、24/25 + αはやがて1に到達することになる。つまり、タイプ7とタイプ11に関してはコラッツ操作を施せば施すほど、どんどん倍率1以下に縮小する数が増えていくのでやがて全てのタイプ7とタイプ11の整数は1に収束する。そして、タイプ15の整数についても同じことが言える。
ただし、タイプ15からタイプ15にループ状に分岐する場合については、証明が済んでいない。この後、タイプ15の連続はその整数が有限の数である限りやがてタイプ7に変容することを証明する。また、2桁の整数に関しては全て1に収束することを証明しているので、全ての整数が有限の整数である限り、小さい整数から順次コラッツ操作を施していけば、1に収束することを証明したことになる。
15タイプからの遷移
タイプ15は、タイプ7かタイプ15の連続かの選択で分岐が始まる。従って、単純に1.5倍される。タイプ15をn回繰り返すと、単純計算では(1.5)n倍で拡大していくことになる。
ここでは、タイプ15の連続から抜け出すことが出来るのかについて議論する。タイプ遷移図を見ると分かる通り、<偶数、15>タイプは次の遷移でタイプ7へ遷移するが、<奇数、15>タイプはタイプ15を繰り返す。
ここからは、an16n+an-116n-1+…+a116+a0を<<<<an,an-1>, an-2>, …, a1>, a0>と表記して計算を行うこととする。ここまでは( )と< >を分けて説明の便宜を図っていたが、これ以降は表現を簡略化する目的で< >と表現することとする。
タイプ15は次のように遷移する。
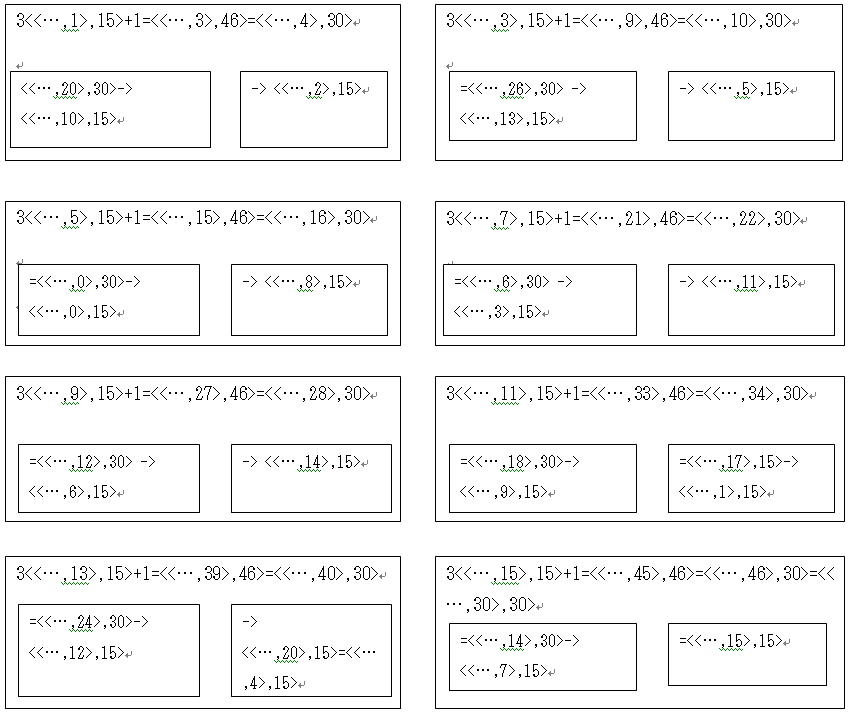
タイプ15でも、<<…, 1>,15>, <<…,5>, 15>, <<…,9>, 15>, <<…,13>, 15>タイプの整数は1回のコラッツ操作で次に、<偶数,15>タイプに遷移しているので、次の操作でタイプ7へと遷移するはずである。
問題は<<…, 3>, 15>, <<…, 7>, 15>, <<…, 11>, 15>, <<…, 15>, 15>タイプである。
このうち、<<…, 3>, 15>と、<<…, 11>, 15>の2つのタイプは問題ない。なぜなら、<<…, 3>, 15>タイプは、次の操作で<<…, 5>, 15>あるいは<<…, 13>, 15>となるので、次の操作で<偶数, 15>タイプとなり、更にその次の操作で、タイプ7へと遷移する。<<…, 11>, 15>も同様に、次の操作で<<…, 1>, 15>あるいは<<…, 9>, 15>タイプへの遷移し、更に次の操作で<偶数, 15>となり、その次にタイプ7へと遷移する。
<<…, 7>, 15>タイプは次の操作で、<<…, 3>, 15>あるいは<<…,11>, 15>タイプとなる。そして、上で説明したように、<<…, 3>, 15>は、<<…, 5>, 15>あるいは<<…, 13>, 15>となり、次の操作で<偶数, 15>となり、更に次の操作でタイプ7へと遷移する。<<…, 11>, 15>についても同じように、<<…, 1>, 15>あるいは<<…, 9>, 15>となり、次に<偶数, 15>タイプとなり、タイプ7への遷移することが出来る。
問題は<<…, 15>, 15>タイプである。このタイプは<<…, 7>, 15>あるいは、<<…, 15>, 15>タイプへ遷移する。<<…, 7>, 15>タイプは既に説明したようにやがてタイプ7へと遷移することが分かっている。
ところが、<<…, 15>, 15>のように15が連続してしまうと、タイプ15から抜け出すことが出来ない可能性がある。次にこの点を確認しよう。
15が最小桁から連続する場合についての考察
15が最小桁から連続する場合は、3n+1の処理をする際の最小桁の45+1=46と、途中桁の46を桁上がりさせる時の上の桁への「+1」が全く同じ動作をしている(45+1=46となり、これが更に上の桁への桁上がりを誘導する)。このため、桁上がりさせた後に元の桁が46-16=30となり、これに対して2で割る処理が加わるため、15となってしまう。
タイプ15の連続からの脱却
各桁の係数が15である場合は一見すると、永遠に1.5倍が続いてしまうように思えるが、そうではない。コラッツ予想では有限の整数を対象としているので、先頭桁というものが必ず存在している。そして、先頭桁の1つ前は0である。つまり、<<<<<<0, 15>, 15>, …>, 15>となっているはずである。これは、<偶数, 15>ということになるので、次のコラッツ操作で、タイプ7へと遷移する。
15タイプから如何にして抜けるかについては、次に図解する。<<<0, 15>, 15>, …>, 15>から、15の並びが1つ減り、15だったところが偶数に変化するまでに4回のコラッツ操作を要していることが分かる。つまり、<<<0, 15>, 15>, …>, 15>は、<<<偶数, 15>, 15>, …>, 15>なので、1回の操作で1つ減り、<<<1, 7>, 15>, …>, 15>になり、ここから<<<…, 偶数>, 15>, …>, 15>に遷移するまでに3回の操作が必要で、合計4回で1つ15の連続列の長さが減ることになる。従って、前に挙げた例の100桁の整数で全ての桁が15の整数の場合は、15の連続から抜け出すまでに、おおよそ(1.5)400倍に拡張することになる。
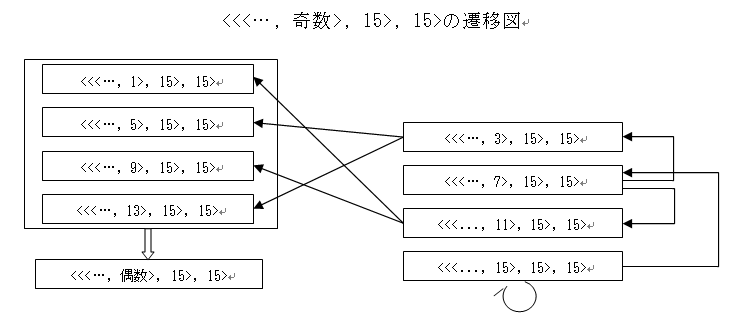
以上、最小桁から15が続いている場合について検討した。
途中にある15についての考察
最小桁から15が連続している場合については厄介であるが、途中で15が出現することもある。これについてはどのように考えたらいいのだろうか。例えば<<<<…, (0から14のいずれか)>, 15>, 15>, (0から14のいずれか)>、…>のような場合である。最小桁が、1、9、13、5のいずれかの場合は、後で2で割る処理が、2回(1と9の場合)、3回(13の場合)、4回(5の場合)あるので、途中にある15は直ぐに他の数に変化してしまう。7、11、15の場合も15の命は短い。そもそも、最小桁から15が続く場合にどうして15が連続してしまうかというと、(3n+1)/2の処理の際の「+1」の処理と同じ作用を、15の桁上がりが果たしてしまうからである。15×3+1=46で、16を桁上がりさせると、最小桁は30となり、その上の桁が45+1=46となり、この桁もさらに上の桁への桁上がりで、30となり、上の桁は45+1=46となって、また桁上がりが発生してしまう。そして、最終的に2で割る処理をすると、30の並びが、全部15へと変わってしまうためである。しかし、途中にある15の場合は、下の桁からの桁上がりがあるとは限らないので、事情が異なる。途中にある15は3倍され、45になるが、下の桁からの桁上がりが期待できないこともある。その場合は、2で割る処理の際に桁間の調整で、46/2=23となり、23=16+7で7になることもあるし、44/2=22となり、22=16+6で6になることもある。あるいはたまたま下からの桁上がりがあって、その結果46になり、更に自分自身が桁上がりして、30になり、2で割る処理で15になることもある。しかし、これもこの時限りのことである。なぜなら、これは2で割る処理が2回の、タイプ7、タイプ11、タイプ15に特有の事情であり、タイプ7は次にタイプ11か、タイプ3となり、タイプ11は次にタイプ1かタイプ9になる。また、タイプ3は次にタイプ5あるいはタイプ13となるので、2で割る処理が1回だけという場合は、ずっと続くわけではないからである。もちろん、タイプ15が最小桁にある場合は例外であるが、これが永遠と続くわけではないことは既に説明したところである。また、今までなかったところに突然15が出現する場合もあるがそれもいつの間にか消滅してしまう。
従って、最小桁から連続している15以外は、途中桁にある15は2、3回のコラッツ操作の間にすぐに消滅してしまうことが分かる。
他のタイプから15タイプへの遷移
15タイプ以外から、15タイプに遷移することがある。タイプ遷移図を見ると、<偶数, 9>-<t, 14>で、tが奇数の時<u, 15>に遷移する。更に、<奇数, 13>-<t, 12>で、tが奇数の時<u, 14>なり、更にuが奇数の時、<v, 15>に遷移している。
<偶数, 9>-<t, 14>(t:奇数)-<u, 15>の遷移では、<0, 9>, <2, 9>, <4, 9>, <6, 9>, <8, 9>, <10, 9>,<12, 9>, <14, 9>のうち、第2桁に因数2が2つ以上入っている<0, 9>, <4, 9>, <8, 9>, <12, 9>はタイプ7へ遷移することが分かる。これに対して、第2桁に因数2が1つしか入っていない<2, 9>, <6, 9>, <10, 9>, <14, 9>はタイプ15を維持する。
3<2, 9> + 1 = <6, 28> → <3, 14> = <2, 30> → <1, 15>
3<6, 9> + 1 = <18, 28> → <9, 14> = <8, 30> → <4, 15>
3<10, 9> + 1 = <30, 28> → <15, 14> = <14, 30> → <7, 15>
3<14, 9> + 1 = <42, 28> → <21, 14> = <20, 30> → <10, 15>
以上より、<2, 9>と<10, 9> だけが、<奇数, 15>となり、15タイプを繰り返すことになる。このうち<2, 9>は<1, 15>となり、更に<1, 15>は、タイプ15の遷移表を確認すると、次のコラッツ操作で<偶数, 15>となり、15タイプから脱出することが出来る。これに対して、<7, 15>は、<<…, 11>, 15>あるいは、<<…, 3>, 15>となり、このうち<<…, 11>, 15>は、<<…, 1>, 15>あるいは<<…, 9>, 15>に、<<…, 3>, 15>は<<…, 5>, 15>あるいは、<<…, 13>, 15>となる。従って、<偶数, 15>になるまでに3回のコラッツ操作を必要とし、15タイプを抜けるまでにさらに1回で計4回の操作を必要とする。
<奇数, 13>から<t, 12>(t:奇数)へ分岐し、更に<u, 14>(u:奇数)へ分岐する遷移では、<1, 13>, <3, 13>, <5, 13>, <7, 13>, <9, 13>, <11, 13>, <13, 13>, <15,13>のうち<奇数、15>となるのは、<15, 13>のみである。
3<1, 13> + 1 = <3, 40> = <4, 24> → <1, 6> = <0, 22> → <0, 11>
3<3, 13> + 1 = <9, 40> = <10, 24> → <5, 12> = <4, 28> → <1, 7>
3<5, 13> + 1 = <15, 40> = <16, 24> → <2, 3>
3<7, 13> + 1 = <21, 40> = <22, 24> → <11, 12> = <10, 28> → <5, 14> = <4, 30> → <2, 15>
3<9, 13> + 1 = <27, 40> = <28, 24> → <7, 6> = <6, 22> → <3, 11>
3<11, 13> + 1 = <33, 40> = <34, 24> → <17, 12> = <16, 28> → <4, 7>
3<13, 13> + 1 = <39, 40> = <40, 24> → <5, 3>
3<15, 13> + 1 = <45, 40> = <46, 24> → <23, 12> = <22, 28> → <11, 14> = <10, 30> → <5, 15>
<5, 15>はタイプ15の遷移表を確認すると、次のコラッツ操作で<偶数, 15>となり、更に次の操作でタイプ7に遷移することが分かる。
2桁の数について、コラッツ予想が成り立つことの証明
本稿では、小さい整数から順次コラッツ予想が正しいことを証明できていると仮定しているので、ここでは<0, 3>から、<15, 15>までの整数について計算して、<1, 0> → <0, 1>に収束することを示す。証明は、こちらを参照のこと。
<1, 5>を除くと、<0, 3> ~ <15, 15>の全ての奇数は最後に<0, 1>に収束する前に、<0, 5>となり、次の操作で、3<0, 5> + 1 = <0, 16> = <1, 0>となっている。<1, 5>の場合は、3<1, 5> + 1 = <3, 16> = <4, 0> → <1, 0>となる。例外的に<0, 21>は3<0, 21> +1 = 64 → 32 → 16 = <1, 0> → <0, 1>となる。したがって、<0, 3> ~ <15, 15>の全ての整数が<0, 1>に収束する前に一旦<1, 0>になっていることが分かる。この時、最小桁がカットできるので、全体として桁が1つずつ小さい方にずれることになる。
結論
「タイプ別の縮小と拡大の概略」以降では出発点となる整数がタイプ1、(3)、(5)、(9)、(13)の時は必ず縮小して出発点となった整数よりも小さい整数にまで縮小することを証明した。また、出発点がタイプ7、(11)、(15)の時にも、減少傾向列に進む分岐の方が、拡大傾向列の分岐の割合よりも多いことを示し、最終的に倍率1以下にまで収束することを示した。そして、タイプ15についてもいずれタイプ7になることを示した。このことから、どのような整数からを出発点としても、コラッツ操作の結果、出発点となる整数よりも小さい値にまで縮小することが分かった。
今、2桁の整数については、小さい整数から順にコラッツ操作を施した場合は、出発点となった整数よりも小さい値は全て1に収束することが分っている。更に、「タイプの変化による縮小と拡大」で説明したことを3桁の整数に関しても小さい整数の順に当てはめていくと全て出発点となった整数よりも小さく縮んでいくことが分かる。4桁の整数、5桁の整数、6桁の整数でも全く同じである。この方法で、小さい順に順次計算していくと、たとえどんなに大きな整数でも、それが有限の整数、つまり最上位の桁に0が付いている整数である限り、必ず1に収束することが言える。<証明終わり>

コメント