コラッツ予想の証明（再々改定版）

再々改訂版　2025/05/28

再改定版　2025/05/24

著者　久米原　栄

コラッツ予想とは

　コラッツ予想とは、任意の正の整数を選んで、nが偶数なら2で割り、nが奇数なら3を掛けて1を足すという操作を繰り返すと、どんなnから始めても有限回の操作で1に辿り着くという主張である。

証明の要約

　任意の正の整数を16を基数としてa_n16ⁿ+a_n-116^n-1+…+a₁16+a₀と表す(a_n, a_n-1, … a₁, a₀は0から15までの整数とする）。ある任意の正の整数に対して、コラッツ操作を施す時に、それが偶数なら、その偶数が含んでいる因数2の個数分「2で割る」処理をして、奇数を取り出すという処理は、コラッツ操作の前処理として考えている。このように考えると、コラッツ操作の対象となるのは奇数であるということになる。もちろん、計算処理の途中で偶数が現れることはある。奇数nに対して、(3n+1)/2の処理をして得られた答えに対して、更に「割る2」の処理が可能ならば、「割る2」の処理をして、答えから因数2を取り除くという一連の処理をコラッツ操作1回分として計算することとする。

　コラッツ操作の対象を奇数として、16を基数とする表現で表すと、最小桁によってタイプ分けすることが出来る。つまり、あらゆる正の奇数は、タイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15の8つのタイプに分けることが出来る。

　任意の整数にコラッツ操作を施すと、タイプ毎に同じ動きをする。そして、あるタイプから別のタイプに遷移する。このタイプ遷移をグラフに表すことが出来る。これを本稿ではタイプ遷移図と称している。タイプ遷移図はどのタイプからどのタイプに遷移するかをグラフ化したものとなる。あるタイプから別のタイプに移るときにいくつかの分岐先がある。2つに分岐する場合、4つに分岐する場合、8つに分岐する場合などである。

　タイプからタイプへの遷移では、最小桁が奇数になっているが、分岐の途中のタイプ内の処理では、偶数となっている。3n+1の計算をしたときに、最終桁に因数2が1つ含まれるか、2つ含まれるか、3つ含まれるかである。ただし、タイプ5のようにタイプ5の中でのコラッツ操作の結果、因数2が4つ以上含まれることもある。

　(3n+1)の結果、最小桁の因数2が1つのときは割る2の処理を1回しかすることが出来ないので、コラッツ操作での結果は、3/2となる（タイプ3、タイプ7、タイプ11、タイプ15）（3n/2ではなく(3n+1)/2なので正確には約3/2であるが、今後の説明ではこの「約」は大勢には影響ないので省略している）。これに対して、因数2が2つ含まれる時（タイプ1、タイプ9）は、3/4となり、因数2が3つ含まれる時（タイプ13）は、3/8となる。更に、タイプ5は自身の処理の中で最低でも3/16となる。

　因数2が1つの場合は、分岐は1回、分岐先は２つとなる。因数2が2つのときは、分岐は2回、分岐先は4つ、因数2が3つのときは、分岐が3回で、分岐先は８つとなる。つまり、タイプ遷移図は2分木の構造を持つ。どの分岐先に行くのかは、下から2つ目の桁の偶数、奇数の違いによる。因数2が2つある場合は、一旦割る2をした段階で、最小桁はまだ偶数である。これは、仮のタイプといってよい。この時の下から2桁目の偶数、奇数によって、更に分岐先が決まることになる。因数2が3つ含まれるタイプは、2回目の割り算によっても、まだ最小桁は、偶数である。従って、この時の下から2桁目の偶数、奇数によって更に枝分かれすることになる。

　2桁の整数にコラッツ操作を施してみると全ての数が1に収束することが分かった。1に収束するまでに必要なコラッツ操作の回数は、多い場合は46回、少ない場合は1回である。そして、末尾2桁の数の並びが同じ2桁の整数と3桁の整数ペアの動きを観察してみると、最初の数回のコラッツ操作では、タイプ（最小桁の数）と第2桁が同じ場合もあり、タイプは同じだが第2桁は異なり偶奇だけは同じという場合があることが分かった。この時は、2桁の整数と3桁の整数のペアは、タイプ遷移図上の同じルートを辿る。しかし、何回かのコラッツ操作の後に、2つのペアの第2桁の偶奇が異なってしまうことがある。こうなると、分岐先としてタイプ遷移図上の異なったルートが選択されることになる。

2つのペア同士の第2桁の偶奇が逆転してしまうのは、3桁の整数の第3桁の奇数の影響である。第3桁が奇数の時は、タイプ間での遷移の際の(3n+1)/2の操作と、タイプ内での分岐の操作を行うための「割る2」の処理で、桁上がり、桁下がりの微調整が必要となる。例えば、タイプ内の「割る2」の処理をするために、その前段階の微調整として、a₂はa₂-1としてa₁+16とするか、a₂+1として、a₁-16とするかの処理が必要となる。そしてこの後、「割る2」をすると、第2桁にはその効果として「+8」あるいは、「-8」という影響が残ることになる。次の操作時でも、第3桁が奇数だと、残る影響は「+8+4」、「+8-4」、「-8+4」、「-8-4」となる。まだ、第2桁の偶奇には影響は与えない。しかし、第3桁が奇数の影響は段々と累積するとやがて「+8+4+2+1」、「+8+4+2-1」、「+8+4-2+1」、「+8+4-2-1」、「+8-4+2+1」、「+8-4+2-1」、「+8-4-2+1」、「+8-4-2-1」、「-8+4+2+1」、「-8+4+2-1」、「-8+4-2+1」、「-8+4-2-1」、「-8-4+２+1」、「-8-4+２-1」、「-8-4-2+1」、「-8-4-2-1」となり、第2桁の偶奇に影響を与えてしまう。これは、タイプ間での(3n+1)/2の「割る2」でも、ほとんど同じような影響を与えることが分かった。第2桁の偶奇に影響が及べば、そこから先は、2つのペアのタイプ遷移図上のルートが異なることになる。つまり、末尾2桁が同じ2桁の整数と3桁の整数のペアは、コラッツ操作を施す度にタイプと第2桁を変化させるが、末尾2桁の偶奇が一致している限り、同じタイプに遷移するが、第2桁の偶奇に影響が及べば、遷移先がお互いに異なるタイプとなってしまう。同じルートを通る限り、その間の縮小・拡大は2桁の整数も、3桁の整数も全く同じである。

　第3桁の奇数の影響がないのは4回までである。コラッツ操作の際に第3桁が奇数という状態が4回続いたとしても、奇数の影響は発揮されない。その間に、第3桁が偶数という回が挟まれば、影響のない状態が4回よりも増えることになる。5回目、6回目まで分岐に影響が出ない可能性も高い。そこで、2桁の整数が何回のコラッツ操作で1に収束するか検証してみた。0x16+3~15×16+15までの128通り（0x16+1~15×16+15までの128通りのうち、0x16+1を除いて127通りだが、ここでは簡単のために128通りとしておくことにする）のうち4回目までに1に収束してしまうものは、20/128=5/32あることが分かった。5回目、6回目までに1に収束してしまうものを合わせると32/128=1/4ある。更に、場合によっては7~9回目までに1に収束してしまうものを含めてもよいかも知れない。しかし、それは確実には分からない。それは、上位桁（この場合は第3桁）の偶数・奇数次第となる。しかし、コラッツ操作を施す度に第3桁が奇数になってしまうという場合だとしても、5/32、平均的には1/4は第3桁の奇数の影響が累積するまでに、1に収束してしまうことになる。例えば、2桁の整数を乗り合いバス、第3桁の整数を乗客だと考えてみよう。乗客は下2桁が自分と同じバスに乗って、途中で第2桁の偶奇が異なってしまったら、そこでバスを降りて、また下2桁が同じバスに乗り換えると考えることにすればどうだろうか。これを何回か繰り返すことで3桁の整数も1に収束することになる。こう考えると、2桁の整数が全て1に収束することが分かれば、3桁の整数も1に収束することが分かる。そして、既に説明したように2桁の整数は最悪でも46回のコラッツ操作で1に収束することが分かっている。4桁の整数についても、末尾3桁が同じ3桁の整数を乗り合いバスに見立てて乗り込めばよい。そして、3桁の整数にまで収束することを証明すれば、その3桁の整数は全て1に収束することが証明済みであるので、4桁の整数も1に収束することが証明できたことになる。このようにして5桁、6桁、7桁の整数についても順次1に収束することを証明することが出来る。従って、たとえどんなに大きな整数から始めたとしても、それが有限の整数である限り、1に収束することが証明できる。

以下証明する）

　任意の整数は、16を基数として、a_n16ⁿ＋a_n-116^n-1+…+a₁16+a₀と表すことが出来る（a_n,a_n-1, …a₁,a₀は0から15までの整数とする）。

　ただし、偶数の場合は、2で割ることで、コラッツ操作の出発点となった整数の半分以下になるので、ここでは奇数について考えることとする。コラッツ操作の出発点となる整数を小さい順に選択して1に収束することを証明して行けば、出発点となった整数よりも小さい整数になるということは、その整数は既に証明済みの整数ということになるからである。

　全ての正の奇数は、16p+1, 16p+3, 16p+5, 16p+7, 16p+9, 16p+11, 16p+15と表現して、これをタイプと考えることとする。つまり、全ての数をタイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15に分類し、これらについてコラッツ操作を施してみよう。

コラッツ操作を施した場合のタイプ毎の動き

　この節では、16p+nを簡略化して(p, n) あるいは、<p, n>と表記することとする。ここでは、コラッツ操作を行う際の「2で割る」処理を「→」で表現している。2で割る処理が複数回続く時も、単に「→」1個で表現している場合があるので注意してほしい。

　ここでは、コラッツ操作の処理途中で、最小桁が偶数の場合は、操作の途中という意味で<p, n>と表現し、最小桁が奇数となり、1回のコラッツ操作が終了した時点で(p, n)という表現を用いている。

●　タイプ1

3(p, 1)+1 = <3p, 4>

　　pが偶数なら、<3p, 4> → <q, 2>

　　　　qが偶数なら、<q, 2> → (r, 1)

　　　　qが奇数なら、<q, 2> → <q-1, 18> → (r, 9)

　　pが奇数なら、<3p, 4> → <3p-1, 20> → <q, 10>

　　　　qが偶数なら、<q, 10> → (r, 5)

　　　　qが奇数なら、<q, 10> → <q-1, 26> → (r, 13)

●　タイプ3

3(p, 3) + 1 = <3p, 10>

　　pが偶数なら、<3p, 10> → (q, 5)

　　pが奇数なら、<3p, 10> → <3p-1, 26> = (q, 13)

●　タイプ5

3(p, 5) + 1 = <3p, 16> = <3p+1, 0> = 16(3p+1) → 3p+1

＊<3p+1, 0> はタイプ別で言えば、タイプ0である。操作の途中で最小桁が0になると、<3p+1, 0> = 16(3p+1)+0 = 16(3p+1) → 8(3p+1) → 4(3p+1) → 2(3p+1) → (3p+1)となり、桁の数字が全体として、1桁小さい方にずれることになるり、倍率的には3/16となっている。ただし、(3p+1)に因数2が含まれている場合もあり、更に倍率が小さくなる可能性もある。

●　タイプ7

3(p, 7) + 1 = <3p, 22>

　　pが偶数のとき、<3p, 22> → (q, 11)

　　pが奇数のとき、<3p, 22> = <3p+1, 6> → (q, 3)

●　タイプ9

3(p, 9) + 1 = <3p, 28>

　　pが偶数のとき、<3p, 28> → <q, 14>

　　　　qが偶数のとき、<q, 14> → (r, 7)

　　　　qが奇数のとき、<q, 14> = <q-1, 30> → <r, 15>

　　pが奇数のとき、<3p, 28> = <3p+1, 12> → <q, 6>

　　　　qが偶数のとき、<q, 6> → (r, 3)

　　　　qが奇数のとき、<q, 6> = <q-1, 22> → (r, 11)

●　タイプ11

3(p, 11) + 1 = <3p, 34>

　　pが偶数のとき、<3p, 34> = <3p+2, 2> → (q, 1)

　　pが奇数のとき、<3p, 34> = <3p+1, 18> → (q, 9)

●　タイプ13

3(p, 13) + 1 = <3p, 40>

　　pが偶数のとき、<3p, 40> = <3p+2, 8> → <q, 4>

　　　　qが偶数のとき、<q, 4> → <r, 2>

　　　　　　rが偶数のとき、<r, 2> → (s, 1)

　　　　　　rが奇数のとき、<r, 2> = <r-1, 18> → (s, 9)

　　　　qが奇数のとき、<q, 4> = <q-1, 20> → <r, 10>

　　　　　　rが偶数のとき、<r, 10> → (s, 5)

　　　　　　rが奇数のとき、<r, 10> = <r-1, 26> → (s, 13)

　　pが奇数のとき、<3p, 40> = <3p+1, 24> → <q, 12>

　　　　qが偶数のとき、<q, 12> → <r, 6>

　　　　　　rが偶数のとき、<r, 6> → (s, 3)

　　　　　　rが奇数のとき、<r, 6> = <r-1, 22> → (s, 11)

　　　　qが奇数のとき、<q, 12> = <q-1, 28> → <r, 14>

　　　　　　rが偶数のとき、<r, 14> → (s, 7)

　　　　　　rが奇数のとき、<r, 14> = <r-1, 30> → (s, 15)

●　タイプ15

3(p, 15) + 1 = <3p, 46>

　　pが偶数のとき、<3p, 46> = <3p+2, 14> → <q, 7>

　　pが奇数のとき、<3p, 46> = <3p+1, 30> → <q, 15>

以上の考察で、タイプ7、タイプ11、タイプ15については、コラッツ操作を1回施すことで3/2倍となり、第2桁の係数が16を超える場合があるが、このことについては別段の考慮はしていない。もし、第2桁の係数が16を超える場合は、第3桁への桁上がりを考えて<<a₂+1, a₁>, a₀>のような記法を導入すべきかもしれないが、このことについては後で言及することとする。現時点では、タイプの遷移について思考を集中するために、第3桁への桁上がりは、無視している。なぜなら、次に示すタイプ遷移図では、最小桁と、下から2番目の桁の数が決定的に重要だからである。

タイプ遷移図

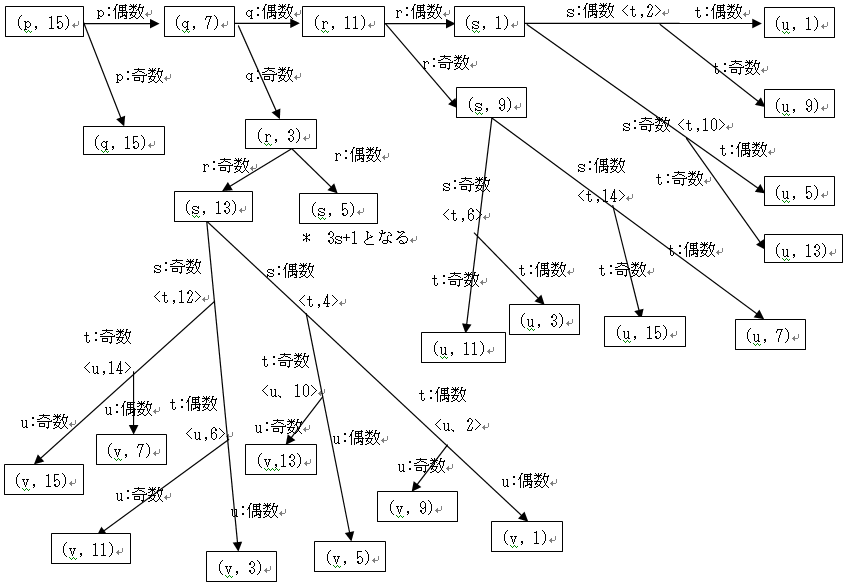
　以上の考察を元にしてタイプ遷移図を描くと次のようになる。

タイプ型と、第2桁の偶数・奇数、3桁以上の整数への拡張

　タイプ遷移を考えた場合に、タイプ型と第2桁の偶数・奇数が決定的に重要な働きをすることが分かった。ここまでは、2桁の整数について論じたが、議論を3桁以上の整数にまで拡張したい。

　下から2番目の桁の数は「2で割る」という処理をする際の微調整の結果を反映している。最小桁が偶数で、第2桁が奇数の場合の処理については既に説明しているので、ここでは最小桁が偶数で、下から3番目の桁（第3桁）が奇数の場合について考えよう。ここで考えるのは、最小桁が偶数で、第2桁も偶数の場合である。第2桁は、最初から偶数なのか、微調整の結果、偶数になったのかはここでは問わないこととする。第3桁が奇数の場合には、第3桁を「-1」して、第2桁を「+16」するか、第3桁を「+1」して、第2桁を「-16」するかのいずれかである。「2で割る」処理が1回のタイプ3、タイプ7、タイプ11、タイプ15の場合は、「2で割る」処理によって、「+8」あるいは、「-8」という結果が残る。つまり、2桁の整数の処理で第2桁が「m」だったとすると、「m+8」あるいは「m-8」となる。「m」の偶奇と、「m+8」あるいは「m-8」の偶奇は全く同じである。ただし、「m」の偶奇については既に2桁の整数の処理の際に解決しているものとして、ここでは問題としない。ここで、議論しているのは、第3桁からの桁下がり、あるいは第3桁への桁上がりであり、その際の「+8」と「-8」である。

　「2で割る」処理が2回必要なタイプ1とタイプ9は、最初の「2で割る」処理の際の状況は「2で割る」処理が1回の時と全く同じである。2回目の「2で割る」処理の際に桁上がりがあれば、1回目の処理で桁上がりしていれば、「n-8」で、ここに桁上がりの「-16」を加えて、それを「2で割る」ので、結果は、「n-4-8」となる。同じように1回目が桁上がりか、桁下がりか、2回目が桁上がりか、桁下がりかで合わせて「n-4+8」、「n+4-8」、「n+4-8」の4通りの結果が得られる。nの偶数・奇数は、「n-4-8」、「n-4+8」、「n+4-8」、「n+4-8」と同じであることが分かる。

　「2で割る」処理が3回必要なタイプ13では、第2桁は2桁の整数の場合がsだとすると、「s-2-4-8」、「s-2-4+8」、「s-2+4-8」、「s-2+4+8」、「s+2-4-8」、「s+2-4+8」、「s+2+4-8」、「s+2+4+8」の8通りとなり、第2桁の偶数・奇数は「s」の場合と同じである。もちろん、タイプ遷移表を見ると、タイプ13は<s, 1>, <s, 9>, <s, 5>, <s, 13>, <s, 3>, <s, 11>, <s, 7>, <s, 15>に分岐し、それぞれの場合について、「s」の値は異なっているが、偶奇については変わりはない。つまり、「s」の偶奇に従って、「s-2-4-8」、「s-2-4+8」、「s-2+4-8」、「s-2+4+8」、「s+2-4-8」、「s+2-4+8」、「s+2+4-8」、「s+2+4+8」の偶奇が決まることになる。

　以上の考察の結果、3桁以上の整数についても、前の節で説明したタイプ遷移図がそのまま適用できるということになる。

タイプ別の縮小と拡大の概略

　タイプ遷移図を見ると、タイプ別の縮小と拡大の概略を知ることが出来る。

　上の図では、タイプ遷移の途中の最小桁が偶数の場合については、<>を、1回のタイプ遷移が完了して、最小桁が奇数になった状態を()を使って表現している。□で囲まれた()型のタイプから()型のタイプへの遷移では、コラッツ操作の対象の奇数nに対して、(3n+1)の処理が施され、この結果は必然的に偶数となるため更に2で割る処理が加えられている。従って、基本的に1回のタイプ遷移で対象となった整数は1.5倍されていることになる。ただし、タイプ遷移の間に<>タイプへの処理が介在している場合、すなわちタイプ1、タイプ9、タイプ13では、「2で割る処理」が更に追加されている。タイプ1と、タイプ9では1回、合計で2回、タイプ13では、追加の処理が2回で、合計3回となる。従って、タイプ1とタイプ9では、(3/2)/2＝3/4、タイプ9では、((3/2)/2)/2=3/8倍となっている。更にタイプ3はタイプ5、あるいはタイプ13に遷移する。タイプ3から、タイプ5への遷移では3/2となるが、タイプ5内の処理では最低でも3/16倍されている。また、タイプ13への遷移でも、3/2となるが、タイプ13から次のタイプへの遷移で、3/8されている。このように考えると、タイプ1、タイプ3、タイプ5、タイプ9、タイプ13では縮小することが分かる。

　拡大するのはタイプ7、タイプ11、タイプ15である。この3つのタイプは(3n+1)/2の処理だけなので、基本的には3/2で拡張する。

　分岐の仕方を見ると、いくつかの類似点がみられる。例えば、(r, 11)-(s, 1)-(u,1) | (u, 9) | (u, 5) | (u, 13)、(r, 11)-(s, 9)-(u,7) | (u, 15) | (u, 3) | (u, 111)と、(s, 13)-<t, 4>-(v, 1) | (v, 9) | (v, 5) | (v, 13) 、(s, 13)-<t, 12>-(v,3) | (v, 11) | (v, 7) | (v, 15)の分岐が全く同じことが分かる。

　また、(r, 3)-(s, 5) | (s, 13)の分岐と、(s, 1)の先の<t, 10>-(u, 5) | (u,13)も同じ、(s, 13)の先の<u, 10>-(v, 5) | (v, 13)も同じである。一見すると、(r, 3)の「3」と<t, 10>, <u, 10>の「10」がマッチしないが、(r, 3)の方は(3n+1)の処理をするので、3×3+1=10となり、マッチする。

　(q, 7)-(r, 11) | (r, 3)と、(s, 13)の先の分岐の<u, 6>-(v, 3) | (v, 11)も同じ、(s, 9)の先の分岐の<t, 6>-(u, 3) | (u, 11)も同じである。これについては、(q, 7)の場合は3×7+1=22で、22=1×16+6で、<u, 6>,<t, 6>の「6」とマッチする。

　(p, 15)-(q, 7) | (q, 15)も、(s, 9)の先の(t, 14)-(u, 7) | (u, 15)、(s, 13)の先の(u, 14)-(v, 7) | (v, 15)と全く同じである。(p, 15)については、3×15+1=46, 46=2×16+14となり、共に「14」となる。

　違いは、タイプからタイプへの遷移では(3n+1)/2の処理が入るが、タイプ内での処理では、「割る2」だけだということである。

　偶数・奇数についてもほとんど同じだが、（s, 13)の内部処理で、1番目、3番目は同じで、一番目が奇数の分岐についてのみ2番目は逆になっている。

　更にタイプ遷移図を眺めてみると、同じタイプが連続する可能性があることである。それは、タイプ1とタイプ13とタイプ15である。タイプ1から、タイプ1への遷移は4つの選択肢のうちの１つであり、しかもタイプの連続の間に3/4に縮小している。タイプ13からタイプ13への遷移は8つの選択肢のうちの1つであり、しかもタイプの連続の間に、3/8に縮小している。従って、タイプ1とタイプ13の連続については、問題とするには当たらない。問題はタイプ15の連続である。タイプ15は連続する間に1.5倍されるので、例えばタイプ15の連続が100回続くと、単純にはその間に(1.5)¹⁰⁰倍されることになるのだが、事はそれほど単純ではなさそうだ。

15タイプからの遷移

　タイプ15は、タイプ7かタイプ15の連続かの1回の選択である。従って、単純に1.5倍される。タイプ15をn回繰り返すと、単純計算では(1.5)ⁿ倍で拡大していくことになる。

　ここでは、タイプ15の連続から抜け出すことが出来るのかについて議論する。タイプ遷移図を見ると分かる通り、<偶数、15>タイプは次の遷移でタイプ7へ遷移するが、<奇数、15>タイプはタイプ15を繰り返す。

　ここからは、a_n16ⁿ+a_n-116^n-1+…+a₁16+a₀を<<<<a_n,a_n-1>, a_n-2>, …, a₁>, a₀>と表記して計算を行うこととする。ここまでは( )と< >を分けて説明の便宜を図っていたが、これ以降は表現を簡略化する目的で< >と表現することとする。

　タイプ15は次のように遷移する。

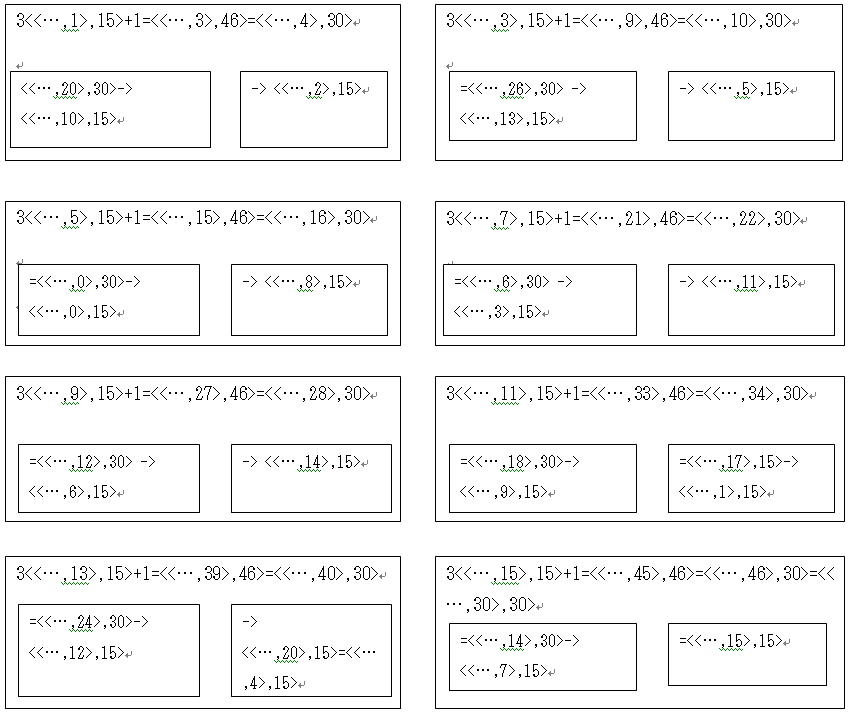
　タイプ15でも、<<…, 1>,15>, <<…,5>, 15>, <<…,9>, 15>, <<…,13>, 15>タイプの整数は1回のコラッツ操作で次に、<偶数,15>タイプに遷移しているので、次の操作でタイプ7へと遷移するはずである。

　問題は<<…, 3>, 15>, <<…, 7>, 15>, <<…, 11>, 15>, <<…, 15>, 15>タイプである。

　このうち、<<…, 3>, 15>と、<<…, 11>, 15>の2つのタイプは問題ない。なぜなら、<<…, 3>, 15>タイプは、次の操作で<<…, 5>, 15>あるいは<<…, 13>, 15>となるので、次の操作で<偶数, 15>タイプとなり、更にその次の操作で、タイプ7へと遷移する。<<…, 11>, 15>も同様に、次の操作で<<…, 1>, 15>あるいは<<…, 9>, 15>タイプへの遷移し、更に次の操作で<偶数, 15>となり、その次にタイプ7へと遷移する。

　<<…, 7>, 15>タイプは次の操作で、<<…, 3>, 15>あるいは<<…,11>, 15>タイプとなる。そして、上で説明したように、<<…, 3>, 15>は、<<…, 5>, 15>あるいは<<…, 13>, 15>となり、次の操作で<偶数, 15>となり、更に次の操作でタイプ7へと遷移する。<<…, 11>, 15>についても同じように、<<…, 1>, 15>あるいは<<…, 9>, 15>となり、次に<偶数, 15>タイプとなり、タイプ7への遷移することが出来る。

　問題は<<…, 15>, 15>タイプである。このタイプは<<…, 7>, 15>あるいは、<<…, 15>, 15>タイプへ遷移する。<<…, 7>, 15>タイプは既に説明したようにやがてタイプ7へと遷移することが分かっている。

　ところが、<<…, 15>, 15>のように15が連続してしまうと、タイプ15から抜け出すことが出来ない可能性がある。次にこの点を確認しよう。

15が最小桁から連続する場合についての考察

　15が最小桁から連続する場合は、3n+1の処理をする際の最小桁の45+1=46と、途中桁の46を桁上がりさせる時の上の桁への「+1」が全く同じ動作をしている（45+1=46となり、これが更に上の桁への桁上がりを誘導する）。このため、桁上がりさせた後に元の桁が46-16=30となり、これに対して2で割る処理が加わるため、15となってしまう。　

タイプ15の連続からの脱却

　各桁の係数が15である場合は一見すると、永遠に1.5倍が続いてしまうように思えるが、そうではない。コラッツ予想では有限の整数を対象としているので、先頭桁というものが必ず存在している。そして、先頭桁の1つ前は0である。つまり、<<<<<<0, 15>, 15>, …>, 15>となっているはずである。これは、<偶数, 15>ということになるので、次のコラッツ操作で、タイプ7へと遷移する。

　15タイプから如何にして抜けるかについては、次に図解する。<<<0, 15>, 15>, …>, 15>から、15の並びが2つ減るまでに4回のコラッツ操作を要していることが分かる。つまり、<<<0, 15>, 15>, …>, 15>は、<<<偶数, 15>, 15>, …>, 15>なので、1回の操作で1つ減り、<<<1, 7>, 15>, …>, 15>になり、ここから<<<…, 偶数>, 15>, …>, 15>に遷移するまでに3回の操作が必要で、合計4回で2つ15の連続列の長さが減ることになる。

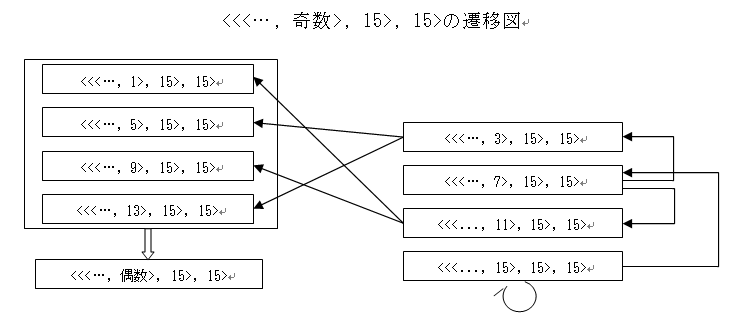
　以上、最小桁から15が続いている場合について検討した。

途中にある15についての考察

　最小桁から15が連続している場合については厄介であるが、途中で15が出現することもある。これについてはどのように考えたらいいのだろうか。例えば<<<<…, (0から14のいずれか)>, 15>, 15>, (0から14のいずれか)、…>のような場合である。最小桁が、1、9、13、5のいずれかの場合は、後で2で割る処理が、2回（1と9の場合）、3回（13の場合）、4回（5の場合）あるので、途中にある15は直ぐに他の数に変化してしまう。7、11、15の場合も15の命は短い。そもそも、最小桁から15が続く場合にどうして15が連続してしまうかというと、(3n+1)/2の処理の際の「+1」の処理と同じ作用を、15の桁上がりが果たしてしまうからである。15×3+1＝46で、16を桁上がりさせると、最小桁は30となり、その上の桁が45+1=46となり、この桁もさらに上の桁への桁上がりで、30となり、上の桁は45+1=46となって、また桁上がりが発生してしまう。そして、最終的に2で割る処理をすると、30の並びが、全部15へと変わってしまうためである。しかし、途中にある15の場合は、下の桁からの桁上がりがあるとは限らないので、事情が異なる。途中にある15は3倍され、45になるが、下の桁からの桁上がりが期待できないこともある。その場合は、2で割る処理の際に桁間の調整で、46/2=23なったり、23=16+7で7になることもあるし、44/2=22となり、22=16+6で6になることもある。あるいはたまたま下からの桁上がりがあって、その結果46になり、更に自分自身が桁上がりして、30になり、2で割る処理で15になることもある。しかし、これもこの時限りのことである。なぜなら、これは2で割る処理が2回の、タイプ7、タイプ11、タイプ15に特有の事情であり、タイプ7は次にタイプ11か、タイプ3となり、タイプ11は次にタイプ1かタイプ9になる。また、タイプ3は次にタイプ5あるいはタイプ13となるので、2で割る処理が1回だけという場合は、ずっと続くわけではないからである。もちろん、タイプ15が最小桁にある場合は例外であるが、これが永遠と続くわけではないことは既に説明したところである。また、今までなかったところに突然15が出現する場合もあるがそれもいつの間にか消滅してしまう。

　従って、最小桁から連続している15以外は、途中桁にある15は2、3回のコラッツ操作の間にすぐに消滅してしまうことが分かる。

他のタイプから15タイプへの遷移

　15タイプ以外から、15タイプに遷移することがある。タイプ遷移図を見ると、<偶数, 9>-<t, 14>で、tが奇数の時<u, 15>に遷移する。更に、<奇数, 13>-<t, 12>で、tが奇数の時<u, 14>なり、更にuが奇数の時、<v, 15>に遷移している。

　<偶数, 9>-<t, 14>(t:奇数)-<u, 15>の遷移では、<0, 9>, <2, 9>, <4, 9>, <6, 9>, <8, 9>, <10, 9>,<12, 9>, <14, 9>のうち、第2桁に因数2が2つ以上入っている<0, 9>, <4, 9>, <8, 9>, <12, 9>はタイプ7へ遷移することが分かる。これに対して、第2桁に因数2が1つしか入っていない<2, 9>, <6, 9>, <10, 9>, <14, 9>はタイプ15を維持する。

3<2, 9> + 1 = <6, 28> → <3, 14> = <2, 30> → <1, 15>

3<6, 9> + 1 = <18, 28> → <9, 14> = <8, 30> → <4, 15>

3<10, 9> + 1 = <30, 28> → <15, 14> = <14, 30> → <7, 15>

3<14, 9> + 1 = <42, 28> → <21, 14> = <20, 30> → <10, 15>

以上より、<2, 9>と<10, 9> だけが、<奇数, 15>となり、15タイプを繰り返すことになる。このうち、<1, 15>はタイプ15の遷移表を確認すると、次のコラッツ操作で<偶数, 15>となり、15タイプから脱出することが出来る。これに対して、<<…, 7>, 15>-<<…, 11>, 15> | <<…, 3>, 15>となり、<<…, 11>, 15>-<…, 1>, 15> | <<…, 9>, 15>, <<…, 3>, 15>-<<…, 5>, 15> | <<…, 13>, 15>となり、<偶数, 15>になるまでに3回のコラッツ操作を必要とし、15タイプを抜けるまでにさらに1回で計4回の操作を必要とする。

　<奇数, 13>-<t, 12>(t:奇数)-<u, 14>(u:奇数)の遷移では、<1, 13>, <3, 13>, <5, 13>, <7, 13>, <9, 13>, <11, 13>, <13, 13>, <15,13>のうち<奇数、15>となるのは、<15, 13>のみである。

3<1, 13> + 1 = <3, 40> = <4, 24> → <1, 6> = <0, 22> → <0, 11>

3<3, 13> + 1 = <9, 40> = <10, 24> → <5, 12> = <4, 28> → <1, 7>

3<5, 13> + 1 = <15, 40> = <16, 24> → <2, 3>

3<7, 13> + 1 = <21, 40> = <22, 24> → <11, 12> = <10, 28> → <5, 14> = <4, 30> → <2, 15>

3<9, 13> + 1 = <27, 40> = <28, 24> → <7, 6> = <6, 22> → <3, 11>

3<11, 13> + 1 = <33, 40> = <34, 24> → <17, 12> = <16, 28> → <4, 7>

3<13, 13> + 1 = <39, 40> = <40, 24> → <5, 3>

3<15, 13> + 1 = <45, 40> = <46, 24> → <23, 12> = <22, 28> → <11, 14> = <10, 30> → <5, 15>

　<5, 15>はタイプ15の遷移表を確認すると、次のコラッツ操作で<偶数, 15>となり、更に次の操作でタイプ7に遷移することが分かる。

最小桁の数（タイプ）の変化による縮小と拡大の実際

　コラッツ操作を施す度に最下位桁の数値（タイプ）が変化していく。最下位桁の数によってタイプ遷移図上のコースが変化していく。ここでは、タイプ遷移図上の分岐点（図では□で囲まれているタイプ）を通るごとに出発点の整数に対してどのように増減しているかを検証し、出発点となった整数に対する倍率を示す。最下位桁の数をnで表し、タイプnからタイプmへの変化を(n)(m)と表現する。

　ただし、この節と、次の「(7)(11)、(11)(1)、(11)(9)からの遷移について」は如何にこの計算が困難であるかの例示であり、証明には結びついていない。証明だけを読みたいという場合は、この2節を飛ばして、「2桁の数について、コラッツ予想が成り立つことの証明」に移っていただきたい#two-digits。

　倍率が1以下になった場合は、そこで出発点の整数よりも小さい整数となったものとして、検証を止めている。小さい整数から順にコラッツ予想が成り立つことを証明していると仮定すると、証明済みの整数となっているからである。

　以降の計算で、倍率が1以下になったものは青で下線を引き、枝葉の分岐で1以下になっている場合は親ノードは青で塗りつぶしている。

(1)(1): 3/4

(1)(5): 3/4

(1)(9): 3/4

(1)(13): 3/4

(3)(5): 3/2 ＊ただし、(5)の中の処理で3/16となるので、合わせて9/32

(3)(13)(1): 3/2 x 3/8 = 9/16

(3)(13)(3): 9/16

(3)(13)(5): 9/16

(3)(13)(7): 9/16

(3)(13)(9): 9/16

(3)(13)(11): 9/16

(3)(13)(13): 9/16

(3)(13)(15): 9/16

(5): 3/16

(7)(3)(5): 3/2 x 3/2 x (3/16) = 27/64 ＊3/16は(5)の中での処理

(7)(3)(13)(1): 3/2 x 3/2 x 3/8 = 27/32

(7)(3)(13)(3): 3/2 x 3/2 x 3/8 = 27/32

(7)(3)(13)(5): 3/2 x 3/2 x 3/8 = 27/32

(7)(3)(13)(7): 3/2 x 3/2 x 3/8 = 27/32

(7)(3)(13)(9): 3/2 x 3/2 x 3/8 = 27/32

(7)(3)(13)(11): 3/2 x 3/2 x 3/8 = 27/32

(7)(3)(13)(13): 3/2 x 3/2 x 3/8 = 27/32

(7)(3)(13)(15): 3/2 x 3/2 x 3/8 = 27/32

(7)(11): 3/2

この時点で1以上なので赤で塗りつぶして、後で検討を加える。

(9)(3): 3/4

(9)(7): 3/4

(9)(11): 3/4

(9)(15): 3/4

(11)(1): 3/2

(11)(9): 3/2

(11)(1)、(11)(9)は赤で塗りつぶして、後で検討する。

(13)(1): 3/8

(13)(3): 3/8

(13)(5): 3/8

(13)(7): 3/8

(13)(9): 3/8

(13)(11): 3/8

(13)(13): 3/8

(13)(15): 3/8

(15)(7): 3/2

(15)(15): 3/2

15についてはやがてタイプ7へと移行するので、ここでは論じない。

(7)(11), (11)(1), (11)(9)からの遷移について

　縮小しないのは、(7)(11)と、(11)(1)、(11)(9)である。(7)(11)は、(7)(11)(1)あるいは、(7)(11)(9)と遷移し、(11)(1)は、(11)(1)(1), (11)(1)(9), (11)(1)(5), (11)(1)(13)へと遷移し、(11)(9)は、(11)(9)(7), (11)(9)(15), (11)(9)(3), (11)(9)(11)へと遷移する。　

●(7)(11)(1)

＞(7)(11)(1)(1): 3/2 x 3/2 x 3/4 = 27/16

＞＞(7)(11)(1)(1)(1): 27/16 x 3/4 = 81/64

＞＞＞(7)(11)(1)(1)(1)(1): 81/64 x 3/4 = 243/256

＞＞＞(7)(11)(1)(1)(1)(5): 81/64 x 3/4 = 243/256

＞＞＞(7)(11)(1)(1)(1)(9): 81/64 x 3/4 = 243/256

＞＞＞(7)(11)(1)(1)(1)(13): 81/64 x 3/4 = 243/256

＞＞(7)(11)(1)(1)(9): 27/16 x 3/4 = 81/64

＞＞＞(7)(11)(1)(1)(9)(7): 81/64 x 3/4 = 243/256

＞＞＞(7)(11)(1)(1)(9)(15): 81/64 x 3/4 = 243/256

＞＞＞(7)(11)(1)(1)(9)(3): 81/64 x 3/4 = 243/256

＞＞＞(7)(11)(1)(1)(9)(11): 81/64 x 3/4 = 243/256

＞＞(7)(11)(1)(1)(5): 27/16 x 3/4 x (3/16) = 81/64 x (3/16) = 243/1,024

＞＞(7)(11)(1)(1)(13): 27/16 x 3/4 x (3/8) = 81/64 x (3/8) = 243/512

(7)(11)(1)(1)と分岐する時は倍率は出発点と比較して1以下になることが分かった。

＞(7)(11)(1)(9): 3/2 x 3/2 x 3/4

＞＞(7)(11)(1)(9)(7): 3/2 x 3/2 x 3/4 x 3/4 = 81/64

＞＞(7)(11)(1)(9)(15): 3/2 x 3/2 x 3/4 x 3/4 = 81/64

＞＞(7)(11)(1)(9)(3): 3/2 x 3/2 x 3/4 x 3/4 = 81/64

＞＞＞(7)(11)(1)(9)(3)(5): 81/64 x 3/2 x (3/16) = 729/2,048

＞＞＞(7)(11)(1)(9)(3)(13): 81/64 x 3/2 x (3/8) = 729/1,028

＞＞(7)(11)(1)(9)(11): 3/2 x 3/2 x 3/4 x 3/4 = 81/64

＞(7)(11)(1)(5): 3/2 x 3/2 x 3/4 x (3/16) = 27/16 x (3/16) = 81/256

＞(7)(11)(1)(13): 3/2 x 3/2 x 3/4 x (3/8) = 27/16 x (3/8) = 81/128

(7)(11)(1)と辿った場合は、(7)(11)(1)(9)(7)と(7)(11)(1)(9)(15)、(7)(11)(1)(9)(11)のみが倍率1以上で、それ以外は全て倍率1以下になっていることが分かる。

●(7)(11)(9)

＞(7)(11)(9)(7): 3/2 x 3/2 x 3/4 = 27/16

＞(7)(11)(9)(15): 3/2 x 3/2 x 3/4 = 27/16

＞(7)(11)(9)(3): 3/2 x 3/2 x 3/4 = 27/16

＞＞(7)(11)(9)(3)(5): 27/16 x 3/2 x (3/16) = 243/512

＞＞(7)(11)(9)(3)(13): 27/16 x 3/2 x (3/8) = 243/256

＞(7)(11)(9)(11): 3/2 x 3/2 x 3/4 = 27/16

●(11)(1)

＞(11)(1)(1): 3/2 x 3/4 = 9/8

＞＞(11)(1)(1)(1): 9/8 x 3/4 = 27/32

＞＞(11)(1)(1)(9): 9/8 x 3/4 = 27/32

＞＞(11)(1)(1)(5): 9/8 x 3/4 = 27/32

＞＞(11)(1)(1)(13): 9/8 x 3/4 = 27/32

＞(11)(1)(9): 3/2 x 3/4 = 9/8

＞＞(11)(1)(9)(3): 9/8 x 3/4 = 27/32

＞＞(11)(1)(9)(7): 9/8 x 3/4 = 27/32

＞＞(11)(1)(9)(11): 9/8 x 3/4 = 27/32

＞＞(11)(1)(9)(15): 9/8 x 3/4 = 27/32

＞(11)(1)(5): 3/2 x 3/4 x (3/16) = 27/128

＞(11)(1)(13) = 3/2 x 3/4 x (3/8) = 27/64

(11)(1)からの分岐については全て倍率1以下になることが分かった。

●(11)(9): 3/2

＞(11)(9)(7): 3/2 x 3/4 = 9/8

＞(11)(9)(15): 3/2 x 3/4 = 9/8

＞(11)(9)(3): 3/2 x 3/4 = 9/8

＞＞(11)(9)(3)(5): 9/8 x 3/2 x (3/16) = 81/256

＞＞(11)(9)(3)(13): 9/8 x 3/2 x (3/8) = 81/128

＞(11)(9)(11): 3/2 x 3/4 = 9/8

　以上の計算結果より、倍率が1以上になってしまう分岐は(7)(11)(1)(9)(7): 81/64、(7)(11)(1)(9)(15): 81/64、(7)(11)(1)(9)(11): 81/64と、(7)(11)(9)(7): 27/16、(7)(11)(9)(15): 27/16、(7)(11)(9)(11): 27/16、(11)(9)(7): 9/8、(11)(9)(15): 9/8、(11)(9)(11): 9/8の9通りであることが分った。

　(11)を起点とする場合は、(11)(9)(7): 9/8、(11)(9)(15): 9/8、(11)(9)(11):9/8のみで、(11)(1)…の遷移は含まれないが、(7)を経由している遷移の場合は、(7)(11)(1)(9)(7): 81/64、(7)(11)(1)(9)(15): 81/64、(7)(11)(1)(9)(11): 81/64のように、…(11)(1)…の場合も含まれている。これは、(7)から遷移した場合の3/2倍が、(11)(1)の遷移の場合の3/4倍を打ち消してしまうためである。

　今まで無視していた(15)タイプの遷移についても考慮すると、(15)から(7)への遷移を追加すればよい（ただし、ここでは(15)から(15)へのループについては除いている）。そうすると、候補として(15)(7)(11)(9)(7)、(15)(7)(11)(9)(15)、(15)(7)(11)(9)(7)と、(11)から(1)を経由して(9)に遷移する(15)(7)(11)(1)(9)(7)、(15)(7)(11)(1)(9)(15)、(15)(7)(11)(1)(9)(7)が候補に挙がって来る。更に、(15)(7)の遷移で3/2倍されるので、(15)(7)(11)(1)(1)(9)(7)、(15)(7)(11)(1)(1)(9)(15)、(15)(7)(11)(1)(1)(9)(7)も候補に挙がって来る。更に(15)(7)(11)(1)(1)(1)(9)(7)、(15)(7)(11)(1)(1)(1)(9)(15)、(15)(7)(11)(1)(1)(1)(9)(7)も候補として考慮しなくてはならない。何故なら、(15)(7)(11)(1)で(3/2)³=(27/8)倍されるので、(1)(1)(9)遷移列で(3/4)²=(9/16)倍だと、(15)(7)(11)(1)の効果を打ち消すには力が足りないと予想されるからである(27/8 x 9/16 = 243/128)。(1)(1)(1)(9)の遷移列では(3/4)³=27/64倍されるので、27/8 x 27/64 = 729/512となり、いくらか緩和される。

　こう考えると、拡張列は次の通りになる。

(7)(11)(1)(9)(7): 81/64、(7)(11)(1)(9)(15): 81/64、(7)(11)(1)(9)(11): 81/64

(7)(11)(9)(7): 27/16、(7)(11)(9)(15): 27/16、(7)(11)(9)(11): 27/16

(11)(9)(7): 9/8、(11)(9)(15): 9/8、(11)(9)(11): 9/8

　さらに列の先頭に(15)を配した列が加わる。

(15)(7)(11)(1)(9)(7): 243/128、(15)(7)(11)(1)(9)(15): 243/128、(15)(7)(11)(1)(9)(11): 243/128、(15)(7)(11)(9)(7): 81/32、(15)(7)(11)(9)(15): 81/32、(15)(7)(11)(9)(11): 81/32

　もちろん、タイプ遷移図を見れば、(11)(9)(7): 9/8、(11)(9)(15): 9/8、(11)(9)(11): 9/8　の列の先頭に(15)を加えることはできないことが分かる。

　これらに加えて、(15)を追加したことによる悪影響を緩和するために(11)(1)の後に、(1)、(1)(1)が加わることになる。こうなると、(15)(7)(11)(1)(1)(9)(7): 729/512 、(15)(7)(11)(1)(1)(9)(15): 729/512、(15)(7)(11)(1)(1)(9)(11): 729/512 、(15)(7)(11)(1)(1)(1)(9)(7): 2,187/2,048、(15)(7)(11)(1)(1)(1)(9)(15): 2,187/2,048 、(15)(7)(11)(1)(1)(1)(9)(11): 2,187/2,048　となる。(11)の後に-(1)(1)(1)(1)が追加されたときは、(15)(7)(11)(1)(1)(1)(1)(9)(7): 6,561/8,192、(15)(7)(11)(1)(1)(1)(1)(9)(15): 6,561/8,192 、(15)(7)(11)(1)(1)(1)(1)(9)(11): 6,561/8,192　となり1以下に収束する。

　先頭に15を追加したためにさらなる問題も出て来る。それは、(15)(7)(3)(13)(11), (15)(7)(3)(13)(7), (15)(7)(3)(13)(15)という列である。(7)(3)(13)(11), (7)(3)(13)(7), (7)(3)(13)(15)であれば、(13)からの遷移で、3/8倍されるため(7)(3)(13)-(1) | (9) | (5) | (13) | (3) | (11) | (7) | (15)の列は27/32倍となって1以下に収束してしまうが、先頭に(15)が追加されると、(15)からの遷移の3/2倍によって3/2 x 27/32 =81/64となって拡張列に転じてしまうためである。ということは、この(15)が列の途中に出現する時にも同様のことが起こることになる。途中に(15)が出現する時は、n x 27/32 > 1で、その(15)までの時点で、倍率が32/27以上の時は、…(15)-(7)(3)(13)-(1) | (9) | (5) | (13) | (3) | (11) | (7) | (15)は3/8倍にも関わらず1以下には収束しないことになる。

　ここからの計算では、大変大きな数が出現するので計算機を使っても計算できない。そこで、次のように計算結果を簡略化した。分子、分母のいずれか大きな数字の桁の数が6桁を越えたら、6桁内に収まるように分子分母の桁をシフトして、小数点以下の数字を四捨五入して、計算結果としている。

　なお、今後の計算で、(5)では、(5)タイプ内の処理で3/16になる場合は、(3/16)と書いて計算している。また、(13)に遷移した時は、(13)からの遷移の結果、倍率が1以下になる場合は(3/8)と書いて計算予測を先取りする形で、記述を簡略化している箇所がある。ただし、(13)からの遷移ではまだ倍率が1以下にならない場合は、その後の計算を考慮して、(13)(1), (13)(3), (13)(5), …, (13)(15)のように具体的に計算を列挙している。

　以上に列挙した21通り（それプラス途中で15が出現する場合）について、最後まで計算をし続ければよいのだが、現時点では無理である。場合分けの数が天文学的に多くなり、計算機の能力を優に超えてしまう。おそらく、計算機がどれだけ発達しても計算機の能力を超えてしまうはずである。それは、15の桁が最小桁から何十兆個、何百京個、何千垓個も並ぶ数はいくらでも簡単にできてしまうからである。

　いずれに場合も、ほとんど同じ分岐であることが分かる。最初の拡大列の倍率が持ち越されることと、最後の遷移が(7)、(15)、(11)のいずれかで違っているだけでほとんど同じことである。何故なら、(7)で終わっているタイプは次に(7)(3)と進むか、(7)(11)と進むかである。(7)(3)と進んだ時は次は、(7)(3)(5)あるいは、(7)(3)(13)と進む。(7)(3)(5)と分岐した場合は、殆どの場合、ここで1以下の倍率に収束してしまう。(7)(3)(13)と進む場合も、3/8倍されるので、ここで収束してしまうことがほとんどであるが、運悪く収束しきれない場合もある。その場合でも更に、(13)-(1) | (9) | (5) | (13)から先に分岐が進めばやがて1以下に収束する。(13)-(3) | (11) | (7) | (15)と進んだ時は、(3)へと分岐した場合以外は茨に道に足を踏み入れることになる。つまり、この場合にも、(7)、(15)、(11)へと分岐することになる。(7)(11)へと分岐した場合でも、(7)(11)(1)へと分岐すれば、何回かの分岐のうちに1以下に収束する。これに対して、難しいのが、(7)(11)(9)と分岐した場合である。この場合も、更に(7)(11)(9)-(7) | (15) | (11)へと分岐すれば、更に難しい道に足を踏み入れたことになる。いずれにしても、-(7) | (15) | (11)への分岐である。しかし、どのように分岐しても、どんなに分岐が深くなっても、必ず1以下に収束すると予想される。それから、どれだけ深く潜っていくかは最終的には、出発点からの拡大列の持つ値の違いである。最初に(11)から出発したものは戻ってきやすいが、3/2で遷移する(7)、(11)、(15)が重なる(7)(11)、(15)(7)(11)は難しくなるが、ただし(11)の後に(1)が続くと、ここで3/4倍されるので、困難さが緩和される。更に(1)(1)と続けばさらに困難さが緩和されることになる。

　最初の拡大列の倍率が大きければ大きいほど、後々の分岐計算では、分岐が深くなるはずである。　

　具体的な分岐計算については、以下を参照のこと。ただし、以下の分岐計算で、1以下に収束することを証明することはできなかった。既に説明したように、分岐の数が天文学的に増えてしまい、おそらく今後どんなに計算機が発達しても無理であろうと推測できる。以下の計算結果は、如何に分岐計算が難しいかを示すためのものにすぎないことをお断りしておく。

　(11)(9)(7): 9/8については、こちら。(11)(9)(15): 9/8については、こちら。(11)(9)(11): 9/8については、こちらを。　

　(7)(11)(1)(9)(7): 81/64以降の分岐はこちらを。(7)(11)(1)(9)(11): 81/64はこちらを。(7)(11)(9)(7): 27/16以降の分岐についてはこちらを、(7)(11)(9)(11): 27/16以降の分岐についてはこちらを参照のこと。

　(15)(7)の列については、こちらを参照のこと。(15)(7)(11)(1)(1)(1)(9)(7): 2,187/2,048、(15)(7)(11)(1)(1)(1)(9)(15): 2,187/2,048 、(15)(7)(11)(1)(1)(1)(9)(11): 2,187/2,048、(15)(7)(11)(1)(1)(9)(7): 729/512 、(15)(7)(11)(1)(1)(9)(15): 729/512、(15)(7)(11)(1)(1)(9)(11): 729/512、(15)(7)(11)(1)(9)(7): 243/128、(15)(7)(11)(1)(9)(15): 243/128、(15)(7)(11)(1)(9)(11): 243/128、(15)(7)(11)(9)(7): 81/32、(15)(7)(11)(9)(15): 81/32、(15)(7)(11)(9)(11): 81/32

　分岐計算では証明が不可能と分かったので、別の道を探すこととする。

2桁の数について、コラッツ予想が成り立つことの証明

　本稿では、小さい整数から順次コラッツ予想が正しいことを証明できていると仮定しているので、ここでは<0, 3>から、<15, 15>までの整数について計算して、<1, 0> → <0, 1>に収束することを示す。証明は、こちらを参照のこと。

　<1, 5>を除くと、<0, 3> ~ <15, 15>の全ての奇数は最後に<0, 1>に収束する前に、<0, 5>となり、次の操作で、3<0, 5> + 1 = <0, 16> = <1, 0>となっている。<1, 5>の場合は、3<1, 5> + 1 = <3, 16> = <4, 0> → <1, 0>となる。例外的に<0, 21>は3<0, 21> +1 = 64 → 32 → 16 = <1, 0> → <0, 1>となる。したがって、<0, 3> ~ <15, 15>の全ての整数が<0, 1>に収束する前に一旦<1, 0>になっていることが分かる。この時、最小桁がカットできるので、全体として桁が1つずつ小さい方にずれることになる。

15タイプを抜け出した時にどうなるのか？

　<<15, 15>, 15>のように最小桁から、15が並んでいる場合に、最上位桁は、0、つまり偶数と考えることが出来る。そして、15の並びが1つ崩れる時に、その崩れた桁は必ず7になっている。その後、15の連続数はしばらく変わらないが、また1つ15が崩れるとき、その桁は7となるはずである。このように考えると、15の連続が0になった時点では、必ずタイプ7になっている。例えば、<<15, 15>, 15>は15の連続から抜け出した時に、<<<<2, 6>, 7>, 1>, 7>となっている。これは、<<<15, 15>, 15>よりも大きな整数である。しかし、<<<<2, 6>, 7>, 1>, 7>にコラッツ操作を施し続けると<<<<2, 6>, 7>, 1>, 7>よりも、小さな値に収束することが予想される。

　それでは、<<<<2, 6>, 7>, 1>, 7>がどのように変化していくか見てみよう。

3<<<<2, 6>, 7>, 1>, 7> + 1 = <<<<6, 18>, 21>, 3>, 22> = <<<<6, 18>, 21>, 4>, 6> = <<<<6, 18>, 20>, 20>, 6> → <<<<3, 9>, 10>, 10>, 3>

3<<<<3, 9>, 10>, 10>, 3> + 1 = <<<<9, 27>, 30>, 30>, 10> = <<<<9, 28>, 14>, 30>, 10> = <<<<10, 12>, 14>, 30>, 10> → <<<<5, 6>, 7>, 15>, 5>

3<<<<5, 6>, 7>, 15>, 5> + 1 = <<<<15, 18>, 21>, 45>, 16> = <<<<15, 18>, 21>, 46>, 0> = <<<<15, 18>, 22>, 30>, 0> = <<<<16, 2>, 22>, 30>, 0> → <<<<8, 1>, 11>, 15>, 0> = <<<8, 1>, 11>, 15>

ここで、<<<<2, 6>, 7>, 1>, 7>よりも小さな値にまで縮小していることが分かる。

　ここで注意すべきことは、下から2桁目の値は上の桁への桁上がりや、2で割るときの調整として桁下がりがあるということである。しかし、いずれの場合も、16が引かれるか足されるかのいずれかであり、2桁の計算結果で下から2桁目が偶数の場合は、第3桁への桁上がり、3桁目からの桁下がりがあった時も偶数で、2桁の計算結果で下から2桁目が奇数の場合は、3桁以上がある時も奇数である。

次に、2桁の<1, 7>の遷移を確認してみよう。

3<1, 7> + 1 = <3, 22> = <4, 6> → <2, 3>

3<2, 3> + 1 = <6, 10> → <3, 5>

3<3, 5> + 1 = <9, 16> = <10, 0> → <5, 0> = 5 x 16 → 5

3<0, 5> + 1 = <0, 16> = <1, 0> → 1

　<<<<2, 6>, 7>, 1>, 7>にコラッツ操作を施した時に、第3桁に着目すると、(…7>, 1>, 7>) – (…10>, 10>, 3) – (…7>, 15>, 5>)と遷移し、その後タイプ0となっている。これに対して、<1, 7>はというと、(<1, 7>)-(<2, 3>)-(<3, 5>)と遷移してその後タイプ0となっている。　

　最下位桁からの15の連続から抜け出した結果の整数にコラッツ操作を施していった場合、下から2番目の偶数奇数が同じで、最下位桁の数が同じというのは、3桁の15の連続から抜け出した結果得られた<<<<2, 6>, 7>, 1>, 7>に対するコラッツ操作に特有のことなのか、それとも一般的なことなのか。

　ここで注視すべきなのは、最初のコラッツ操作を施した時、第3桁は「7」で奇数だということである。その後、第3桁が偶数の場合も交じっている。<<<15, 15>, 15>, 15>が15の連続から脱出した時は、<<<<12, 2>, 9>, 14>, 9>, 7>で、第3桁は偶数になっている。

　第2桁はコラッツ操作をするたびに「2で割る」処理をするために桁間の値の調整をする。この時、最小桁と、第2桁、第3桁が共に偶数の場合は、第2桁は、2桁の整数と、3桁以上の整数では変わりがない。しかし、第3桁が奇数の場合は、桁の調整のために、第2桁は桁上がりが発生してその結果、第2桁が「-16」され、第3桁が「+1」されるか、逆に第3桁からの桁下がりが発生して、第3桁が「-1」され、その結果第2桁が「+16」されるかのいずれかの状況が発生する。つまり、コラッツ操作を行い「割る2」の処理を行う際に、桁上がり、桁下がりが発生してしまうために、第2桁の数に変化が現れるということだ。この「2で割る」処理の際の桁間の調整が2回行われると、1回目の「+16」、「-16」の効果は「+8」、「-8」となるが、新たな「+16」、「-16」の効果と合算すると「+16+8」、「+16-8」、「-16+8」、「-16-8」となり、ここで「割る2」の処理をすると、「+8+4」、「+8-4」、「-8+4」、「-8-4」第2桁の偶数・奇数には影響がない。

3回目には、「+16+8+4」、「+16+8-4」、「+16-8+4」、「+16-8-4」、「-16+8+4」、「-16+8-4」、「-16-8+4」、「-16-8-4」となり、「割る2」の処理をすると、「+8+4+2」、「+8+4-2」、「+8-4+2」、「+8-4-2」、「-8+4+2」、「-8+4-2」、「-8-4+2」、「-8-4-2」となり、依然として、第2桁の偶数・奇数は同じである。4回目は、「+16+8+4+2」、「+16+8+4-2」、「+16+8-4+2」、「+16+8-4-2」、「+16-8+4+2」、「+16-8+4-2」、「+16-8-4+２」、「+16-8-4-2」、「-16+8+4+2」、「-16+8+4-2」、「-16+8-4+2」、「-16+8-4-2」、「-16-8+4+2」、「-16-8+4-2」、「-16-8-4+2」、「-16-8-4-2」となって、「割る2」の処理を加えると、「+8+4+2+1」、「+8+4+2-1」、「+8+4-2+1」、「+8+4-2-1」、「+8-4+2+1」、「+8-4+2-1」、「+8-4-2+1」、「+8-4-2-1」、「-8+4+2+1」、「-8+4+2-1」、「-8+4-2+1」、「-8+4-2-1」、「-8-4+２+1」、「-8-4+２-1」、「-8-4-2+1」、「-8-4-2-1」のように第2桁の偶数・奇数が反転してしまうことになる。第2桁の偶数・奇数が反転してしまうと、その後のルートが変わって違うタイプに遷移してしまうことになるので、末端の2桁が<1, 0>になる前に、違うタイプへの遷移が発生してしまえば、その新たなタイプからやり直しということになる。

　偶数・奇数の反転によるタイプ遷移の変換は、タイプ1とタイプ9、タイプ5とタイプ13、タイプ7とタイプ15、タイプ3とタイプ11で起こっていることはタイプ遷移図を見ると確認できる。ただし、「割る2」の処理に伴う偶奇の変換が、タイプ遷移内の処理の中で起こるかもしれないタイプ1とタイプ9のときは、(u, 1) | (u, 9)と(u, 5) | (u, 13)の間、(u, 7) | (u, 15)と(u, 3) | (u, 11)の間でも起こり、更にタイプ遷移内の「割る2」の処理が2回行われるタイプ13内の処理では、［{(u, 1) | (u, 9)} | ｛(u, 5) | (u, 13)｝］| ［｛(u, 7) | (u, 15)} | ｛(u, 3) | (u, 11)｝］の間でも起きる可能性がある。

　もう一度タイプ遷移図を確認してみよう。ここで気がつくのは、既に何度か説明したが、タイプ15をルートとしたツリー構造と部分木のツリー構造が相似形になっていることである。ただし、1カ所だけ相似形が左右反転しているところがある。それは、(s, 9)をルートとした部分木と、(s, 13)配下の<t, 12>の配下の部分木の偶奇が反転していることである。

　ここからは、第2桁が偶数での分岐を(s, 9)e<t, 14>、奇数での分岐を(s, 9)o<t, 6>のように表現することにする。(s, 9)e<t, 14>-e(u, 7) | o(u, 15), (s, 9)o<t, 6>-e(u, 3) | o(u, 11)となるが、(s, 13)の配下の部分木では、<t, 12>e<u, 6>- e(v, 3) | o(v, 11), <t,12>o<u, 14>-e(u, 7) | o(u, 15)となっている。

相似形の破れについて

　(s, 9)をルートとした部分木と、(s, 13)配下の<t, 12>の配下の部分木の偶奇が反転しているのは何故だろうか。

　理由は単純である。タイプ別の分岐についてもう一度考えてみよう。

＜タイプ9＞

3<s, 9> + 1 = <3s, 28>

sが偶数のとき、<3s, 28> → <t, 14>

　　　tが偶数のとき、<t, 14> → <u, 7>

　　　tが奇数のとき、<t, 14> = <t-1, 30> → <u, 15>

sが奇数のとき、<3s, 28> = <3s+1, 12> → <t, 6>

　　　tが偶数のとき、<t, 6> → <u, 3>

　　　tが奇数のとき、<t, 6> = <t-1, 22> → <u, 11>

＜タイプ13＞

3<s, 13> + 1 = <3s, 40>

sが偶数のとき、<3s, 40> = <3s+2, 8> → <t, 4>

sが奇数のとき、<3s, 40> = <3s+1, 24> → <t, 12>

(s, 9)をルートとした部分木では、e<t, 14> | o<t, 6>で枝分かれしているが、(s, 13)の配下の<t, 12>をルートとした部分木では、e<u, 6> | o<u, 14>で枝分かれしている。これは単に、(s, 9)の「9」と(s, 13)の「13」の違いにすぎない。

奇数分岐の効果の累積について

　(s, 13)の配下の<t, 12>まで、第2桁が奇数という状態が3ステップ連続していることに着目してみよう。ここで、<<a₂, a₁>, a₀>という整数について考えてみることにする。<a₁, a₀>については既に検討しているので、a₁の調整が済み、a₁が偶数（a₀は偶数とする）になっていると仮定する。ここで、a₂が奇数で、調整が必要であるという点から話を始めることとする。

　最小桁と第2桁が偶数、あるいは第2桁を偶数に調整する必要があれば調整した後で（ただし、ここまでの調整は既に済んでいると仮定する）、第3桁の調整を行う。<<a₂, a₁>, a₀>で、a₂が奇数の場合は、桁間の調整でa₂はa₂-1、a₁はa₁+16、あるいはa₂+1、a₁-16となる。これを2で割って、第2桁はb₁+8、b₁-8と表現できる。これを再度3倍して、上の桁からの桁下がり、上の桁への桁上がりを考える。例えば、b₁+8の場合は、3b₁+24(これはb₁+8+16と表すことが出来る）となり、「2で割る」とc₁+12となる。これはc₁+4+8と表現することもできる。桁上がり、桁下がりを合わせて考えると、c₁+4+8、c₁+4-8、c₁-4+8、c₁-4-8となる。ここで、問題なのは「b₁」が奇数の場合である。これは、2桁の計算の中で吸収されているはずである。今問題としているのは、第3桁からの桁下がり、あるいは第3桁への桁上がりなので、「b1+8」の「+8」、「3b1+24」の「+24」に着目して議論している。

　タイプ間の遷移で、奇数タイプが連続するのは、2回のみであるが、実は、(q, 7)o(r, 3)o(s, 13)の列の末尾の(s, 13)の最初の処理で、(3n+1)/2の処理を1回行っている。c₁+4+8に対して3回目の処理を施すと、3c₁+12+24となり、これを「2で割る」ことで、d₁+6+12となる。他の表現も合わせると、d₁+6+12、d₁+6-12、d₁-6+12、d₁-6-12となる。これらは、d₁+2+4+4+8、d₁+2+4-4-8、d₁-2-4+4+8、d₁-2-4-4-8と表現することもできる。タイプ間の遷移で、第2桁が奇数の遷移が繰り返されるのは、(q, 7)o(r, 3)o(s, 13)のみで、それ以外はタイプ内での処理が介在している。

　では、タイプ内の処理ではどうか。最初の1回は、(3n+1)/2の処理をするが、2回目、3回目は「割る2」の処理だけである。b₂が奇数の場合は、b₁+8、b₁-8は、b₁+8+16、b₁+8-16、b₁-8+16、b₁-8+16となり、これらを「2で割る」と、c₁+4+8、c₁+4-8、c₁-4+8、c₁-4-8となる。更にc₂が奇数なら、「2で割る」処理をすることで、d₁+2+4+8、d₁+2+4-8、d₁+2-4+8、d₁+2-4-8、d₁-2+4+8、d₁-2+4-8、d₁-2-4+8、d₁-2-4-8となる。

　これから見えることは、タイプ間での(3n+1)/2の処理と、タイプ内での「割る2」の処理では、結果がとても良く似ていることである。タイプ間での処理と、タイプ内での処理の効果が累積すると考えてみよう。(3n+1)/2の処理を3回続けて、次にタイプ内の処理を加えてみよう。

　e₁+1+2+2+4+8、e₁+1+2+2+4-8、e₁+1+2+2-4+8、e₁+1+2+2-4-8、e₁+1-2-2+4+8、e₁+1-2-2+4-8、e₁+1-2-2-4+8、e₁+1-2-2-4+8、e₁-1+2+2+4+8、e₁-1+2+2+4-8、e₁-1+2+2-4+8、e₁-1+2+2-4-8、e₁-1-2-2+4+8、e₁-1-2-2+4-8、e₁-1-2-2-4+8、e₁-1-2-2-4-8となる。

　「2で割る」処理をする際の、上の桁の奇数を偶数に調整するために下の桁への「+16」の桁下がり(a₂-1、a₁+16)、下の桁からの桁上がり(a₂+1、a₁-16)の効果が累積する。このことが、<<<<2, 6>, 7>, 1>, 7>の計算結果が、<1, 7>の計算結果と次第に合わなくなってしまう原因である。つまり、<1, 7>にコラッツ操作を繰り返すと、やがて1に収束するという証明が、<<<<2, 6>, 7>, 1>, 7>にはそのままでは適用できないということになる。

　タイプ間での(3n+1)/2の処理と、タイプ内での「割る2」の処理は、奇数分岐の累積による効果という点について言えば全く同じである。しかも、それは必ずしも連続している必要はないということになると、そのようなタイプ遷移図上でいくつも確認することが出来る。

　第2桁の偶奇が逆転するという現象が起これば、2分木の分岐の部分が逆になってしまう。

　第3桁からの影響と、第4桁からの影響、第5桁からの影響、更に上の桁からの影響がどんどん第2桁まで下りてくることになる。もちろん、第3桁からの影響と比べると、第4桁からの影響は単純に計算すると1/16となっている。更に、第5桁からの影響は1/256となるだろうと思われるが、しかし1に収束するまでのコラッツ操作が何百回、何千回、何万回、何億回になると予測すると決して小さな値ではない。

　第3桁が奇数の影響が4回分累積すると、第2桁の偶奇が反転してしまうが、偶奇が反転しても、その後1回分は枝分かれによる拡大縮小の倍率は同じである。つまり、3回目までは偶奇が反転しないが、4回目で反転する。しかし、4回目は枝分かれしたとしても、拡大縮小の割合が同じなので、4回目までに1に収束してしまえば、末尾の2桁が同じ2桁の整数と、第3桁の整数は同じ倍率で収束することになる。

　2桁の整数にコラッツ操作を施した場合に、最大の試行回数を必要とするのは<14, 7>と<14, 11>の46回である。これに対して4回以内で収束してしまう場合もある。例えば、<0, 5>, <1, 5>, <5, 5>は1回、<0, 3>, <0, 13>, <3, 5>, <7, 1>, <13, 5>, <14, 3>は2回、<1, 1>, <2, 3>, <4, 5>, <4, 11>, <8, 13>は3回、<0, 11>, <1, 7>, <2, 13>, <5, 13>, <11, 5>, <12, 9>は4回で1に収束する。20/128=5/32の割合で4回以内に1に収束してしまう。これは、下位2桁が同じ2桁の整数と3桁の整数のうち5/32は、奇数分岐の累積の効果が分岐の偶奇に影響を与える前に(プラス、同じ拡大縮小率での後1回の試行）、2桁の整数は1に収束し、3桁の整数は2桁の整数に、あるいはコラッツ操作を施す前よりも小さな値にまで収縮すると言える。そして、もし小さい順に1に収束することを証明しているのなら、既に証明済みの整数にまで収縮してしまうことになり、3桁の整数も1に収束することが証明できたことになる。

　これは奇数の分岐が連続した場合を想定しているが、必ずしも奇数分岐が連続している必要はない。実際は、偶数分岐が半分程度交じっているはずなので、5、6回までに1に収束するものは奇数分岐の累積効果が表れる前までに1に収束してしまうはずである。第3桁が偶数の場合は、そのまま「2で割る」処理を行うので、調整のための桁上がり桁下がりが必要ない。第3桁が偶数か奇数かの割合は1:1である。それから、奇数は3倍しても奇数、偶数は3倍しても偶数である。第3桁が偶数の場合、0、2、6は「2で割る」処理をしたあとは奇数となり、4、8は「2で割る」処理をした後も偶数である。それから、第3桁が奇数の場合はどうだろうか。1の場合は調整の結果、0か2となり、2で割ると、5、1となりいずれも奇数となる。3の場合は調整の結果2か4となり、2で割ると1、2となり、偶数か奇数かは1:1の割合である。5の場合は調整の結果4か6となり、2で割ると2、3となり、偶数か奇数かの割合はこれも1:1となる。7の場合は調整の結果は、6か8となり、2で割ると、3、4となり、偶数か奇数かの割合は1:1となる。9の場合は調整の結果、8か0となり、2で割ると、4、5となり、偶数か奇数かの割合は1:1となる。こう考えると、第3桁が奇数となり、「2で割る」処理をする際に桁上がり桁下がりの微調整が必要な割合は、1/2 x 3/5 + 1/2 x 4/5 x 1/2 + 1/2 x 1/5 = 12/20 = 3/5で、微調整が必要ない割合は2/5となる。こう考えると、奇数の効果の累積が効果を発揮するまでには、「3+2」回程度のコラッツ操作ができ、これに「+1」すると、大体「5~6」回程度とするのは妥当なところである。では、5回、6回で1に収束するものはどれだけあるか。5回で収束するのは、<0, 7>, <0, 15>, <1, 13>, <3, 13>, <7, 5>, <15, 1>, <15, 5>で、6回で収束するものは、<0, 9>, <1, 3>, <2, 5>, <9, 5>, <10,3>で、1回で収束するものから6回までに収束するものを合計すると32、32/128＝1/4となる。つまり、最小桁と第2桁が同じ2桁の整数と、3桁の整数の組み合わせのうち、コラッツ操作を何度か施しても、最小桁が同じで、第2桁の偶奇が同じという状態を保ちつつ、2桁の数字が1に収束し、3桁の整数は最小桁が0になるという組み合わせが、確実に言えるものだけでも5/32はあり、大まかな見積もりでは大体1/4程度になるということである。5/32については確実に言えることだが、1/4については「程度」としか言えない。何故かというと、これは上位桁の偶数、奇数の並び方次第だからである。しかし、かなり確度の高い「程度」であることは確かなようだ。

　説明が複雑になるので、説明の仕方を少し簡略化することにする。4回の試行をセットとして考えることとする。このセットでは、このセット内に例えば1～３回で１に収束してしまう場合もあるが、それも併せて考える。４回未満で１に収束してしまうなら、そこで計算を止めればいいということである。

　ここでもう一つ追加すべきことがある。5、6回で1に収束する場合については不確実性が伴うと言ったが、そうでない場合もある。それは、1回目の4回試行セットで1に収束できなかったものでも、「最初の4回試行セットで1に収束する整数」にまで変換されるものがあることである。これらは、仕切り直しの2回目の「4回試行セット」で確実に1に収束すると言ってよい。例えば、5回目までに収束する整数としては、<0, 7>, <0, 15>, <1, 13>, <3, 13>, <7, 5>, <15, 1>, <15, 5>があるが、これらは全て最初の4回試行セットで、「4回目までに1に収束する整数」として挙げた整数にまで遷移している。

　では、6回目までに1に収束するものはどうか。<0, 9>, <1, 3>, <2, 5>, <4, 13>, <5, 1>, <9, 5>, <10, 3>などがある。これらにうち、<1, 3>と<10, 3>は最初の4回試行セットで、「4回目までに1に収束する」整数にまで遷移している。具体的には、<1, 3>は2回の試行で、<0, 11>に遷移しており、<0, 11>は4回の試行で1に収束することが分かっている整数である。また、<10, 3>は、2回の試行で、<1, 7>に遷移する。この<1, 7>は4回の試行によって、1に収束する。それ以外の、<0, 9>, <2, 5>, <4, 13>, <5, 1>, <9, 5>は、最初の4回試行セットで、「最初の4回試行セットで1に収束する」整数にあと1回で遷移する整数である。ただ、4回の試行セットでもう一度ペアの組み直しということになると、せっかくあと少しのところに近づいても、そのことが全く意味を持たなくなってしまう。ただ、もう少しで1に収束してしまう1歩手前なので、起点となった整数からの拡張率はそれほど大きくはなっていないはずである。

　3桁の整数と下2桁が同じ2桁の整数を考えてみよう。コラッツ操作の度にタイプ型が変わり、第2桁の偶奇も変わっていくが、タイプ型と第2桁の偶奇が同じ限り、タイプ遷移図上の同じルートを辿って行く。従って、2桁の数字はある目的地に向かう乗り合いバスのような存在である。3桁の整数は、タイプ型と第2桁の偶奇が同じである限りそのバスに乗って進めばいいが、行き先が違うところで、そのバスを降りると考えてみよう。このタイプ型が同じで、第2桁の偶奇が同じ状態で行われたコラッツ操作の連続を「第3桁が奇数での分岐の効果が4回分累積するまでの連続試行のセット」あるいはもっと短く「奇数効果累積前の一連の連続試行のセット」と呼ぶことにしよう。第3桁の偶奇は平均的には半分半分で出現するはずなので、第3桁が奇数での試行が「4」にまで累積するまでに、通常は5~6回程度と考えるのが妥当だが、7、8回程度の試行が可能ということも当然ある。7回は、<1, 9>, <3, 1>, <3, 3>, <6, 3>, <6, 5>, <12, 5>, <12, 13>, <13, 9>、8回は、<2, 1>, <4, 1>, <4, 3>, <8, 3>, <8, 5>である。

　「奇数効果累積前の一連の連続試行のセット」まで、コラッツ操作を連続的に行い、バスの目的地が異なる分岐点まで来たらそのバスを降りて（もちろん、途中で目的地に着いてしまう場合もあるが、その時はそこで降りることにすればよい）、また別の宛先のバスに乗り換えると考えると、1/4程度はバスから降りた時点で1に収束していることになる。

　「奇数効果累積前の一連の連続試行のセット」で、最初にコラッツ操作を施した時点と異なる整数となっている、と言っても、当然、全くでたらめに整数が選択されるわけではない。タイプ遷移図上では、タイプ1に分岐すべき場合に、タイプ9になり、タイプ9に分岐すべき場合にはタイプ1になるというように規則的に分岐が変わる。このタイプ1とタイプ9のような組み合わせが、タイプ5とタイプ13、タイプ7とタイプ15、タイプ3とタイプ11である。「奇数効果累積前の一連の連続試行のセット」の間に2桁と3桁のペアはタイプ遷移図上の同じルートを通り、「奇数効果累積前の一連の連続試行のセット」の終わりにタイプが変更してしまうということは、タイプによって違いはない。タイプの変換が起り、ペアが解消され新しいペアが作られても、それ以降の「奇数効果累積前の一連の連続試行のセット」は、第1回目の「奇数効果累積前の一連の連続試行のセット」と同様の条件で行われ、同じ結果をもたらす。つまり、1/4は縮小し、3/4は拡大する。

　2桁の整数と3桁の整数のペアが解消された時点で、3/4については1に収束することが出来ない。この時、末尾の整数は変化してしまっているので、この時の末尾2桁の数の並びに従って、3桁の整数は、新しい2桁の数字のペアを選ばなくてはならない。そして、「奇数効果累積前の一連の連続試行のセット」の後にまた新しい乗り物に乗り換えるのだ。どこに進んでいくかは、2桁の整数次第である。ただし、ここで注意すべきことは、1回目の「奇数効果累積前の一連の連続試行のセット」で、1に収束できなかったものについては、大きな整数になってしまっていることである。従って、2回目の「奇数効果累積前の一連の連続試行のセット」で、2桁の整数が1に収束したとしても、それとペアになっている3桁の整数は、2回目の「奇数効果累積前の一連の連続試行のセット」の開始時点、つまり1回目の試行セットの終わりの時点よりも小さくなっているというだけで、1回目の「奇数効果累積前の一連の連続試行のセット」の前の状態よりも小さい値になっているわけではないことだ。つまり、2回目では、1回目の終わりにまで戻すことしかできないので、更にもう1回必要となる。これで1/4が1以下にまで収束することが出来る。

　さらに厄介なことは、3回目までに1以下に収束できない整数に関しては、過去の3回でどんどん大きくなってしまっている場合もある。過去の3回では、1+1+1=3回分拡大している場合、途中で1回縮小している場合（もちろん、残ったものは最初の1回目は拡大しているので、1+1-1=1、あるいは、1-1+1=1。ただし、1-1+1の場合は、もしかしたら2回目で1に収束している可能性も高い）について考えなくてはならない。最悪3回連続で拡大しているとすると、それを元の出発点に戻すまでに、その分の収縮が必要となり、元に戻すだけで3回の「奇数効果累積前の一連の連続試行のセット」が必要となるかもしれない。その上で更に1回縮小させる。これで、残りのうち1/4が1に収束する。と言っても、元に戻す処理から換算すると、(1/4)⁴となる。このように考えると、1に収束せずに拡大していってしまうものについて、元に戻す処理がだんだん大変になっていくことが分かる。

2桁の整数と3桁の整数のペアの収束

　2桁の整数の収束については既に説明したが、そこではコラッツ操作何回で1に収束したかに焦点を当てていた。ここでは、もっと具体的に2桁の整数の収束について考察することとする。

　最初に考えておかなくてはならないことがある。1/4程度は2桁の整数は1に収束し、3桁の整数は最小桁が0になる。この最小桁が0になったということをもって、小さな整数に遷移したと言い切れるのかである。通常の場合は、その整数自体が大きくなっても最小桁が0になることはあり得るからである。しかし、最小桁の2桁が全く同じ、2桁の整数と、3桁の整数のペアで、2桁の整数が1に収束し、3桁の整数の最小桁が0になった時、3桁の整数は実は増加していたということはあり得ないことである。何故なら、末尾2桁が同じ整数同士に「奇数効果累積前の一連の連続試行のセット」を施した時は、タイプ遷移図上の全く同じルートを辿って行く。同じルートを通ると拡大縮小の率は全く同じなので、2桁の整数が1に収束する時に、それとペアの3桁の整数が拡大してしまったということはあり得ないことである。

　1回の「奇数効果累積前の一連の連続試行のセット」の間に5/32は確実に1に収束し、1/4は殆どの割合で1に収束する。それ以外の3/4については拡大すると単純に割り切ってしまったが、果たしてそうなのか。もう一度考えてみたい。例えば、<8, 7>について考えてみよう。<8, 7>は4回の試行によって<2, 11>に遷移し、<2, 11>は3回の試行によって<2, 5>に遷移し、<2, 5>は1回の試行によって<0, 7>に遷移し、<0, 7>は5回の試行によって1にまで収束する。つまり、<8, 7>(transition4)<2, 11>(transition3)<2, 5>(transition1)<0, 7>(transition5)<0, 1>=13回の試行によって1に収束することになる。<8, 7>は上に述べた3/4に該当する整数であるが、自分自身よりも小さい整数に遷移した（ということは既に証明済みの整数）タイミングで、ルート転換をしている。つまり、1度たりとも拡張路線には入らずにひたすら縮小路線を走っているバスだということになる。<8, 7>(transition4)<2, 11>で、出発の起点となっている<8, 7>よりも小さい<2, 11>になっている時点で証明終わりとしてもよい。2桁の整数が起点となった整数よりも小さい値となったということは、ペアとなっている3桁の整数も同じ割合で縮小しているはずで（同じルートを通っているはずなので、拡張・縮小の率は同じ）、その時、証明済みの整数よりも小さい値に縮小していると言える。

　とりあえず、<8, 7>のように6回までの試行を繰り返すことで、1に収束しているものを残りの3/4の中から数えてみよう。ところが実際は、試行のセットとして6回が現れることは、<0, 9>の1例のみである。そして、<0, 9>は5回目に<0, 5>に到達しているので、この時に第2桁が奇数に変わっても<0, 13>に分岐が変更されるだけである。この点をもう少し詳しく見て行こうと思う。<0, 5>に行くはずが第2桁の偶奇の反転で<0, 13>に分岐してしまう場合、拡張路線に乗ってしまう可能性は3/8である（<v, 1> | <v, 9> | <v, 5> | <v, 13> | <v, 3>の5/8は縮小し、<v, 11> | <v, 7> | <v, 15>は拡張）するが、これは一般的な場合である。あと一歩で1に収束するという点まで来ている時は、<0, 13>への分岐は3/2 x 3/8 = 9/16で確実に1まで収束してしまうことになる。このように考えると、試行のセットとして6回が現れる<0, 9>は無視していいということになりそうである。従って、ここでは5回目までの試行セットの繰り返しで1に収束している整数を数えることとする。1/4は合計で6回目までに収束しているものなので、ここでは合計で7回以上の回数を必要とするものの中から、5回までの試行を繰り返すことで1に収束しているものを探してみよう。<1, 9>, <2, 1>, <2, 7>, <2, 11>, <3, 1>, <3, 3>, <3, 9>, <3, 11>, <4, 1>, <4, 3>, <4,15>, <5, 7>, <5, 9>, <6, 3>, <6, 5>, <6, 9>, <7, 3>, <7, 7>, <7, 11>, <8, 3>, <8, 5>, <8, 7>, <8, 11>, <9, 9>, <9, 13>, <10, 13>, <11, 1>, <11, 3>, <11, 9>, <11, 11>, <12, 5>, <12, 11>, <12,13>, <13, 1>, <13, 3>, <13, 9>, <13, 11>, <14, 5>, <14, 13>, <15, 7>, <15, 9>と、41ある。この中で、1~4回の試行の繰り返しだけで1に収束してしまっているものは、<1, 9>, <2, 1>, <3, 3>, <3, 11>, <4, 3>, <5, 9>, <6, 5>, <7, 7>, <8, 5>, <8, 11>, <9, 13>, <11, 1>, <11, 3>, <11, 9>, <11, 11>, <12,13>, <13, 1>, <13, 3>, <13, 9>, <14, 13>, <15, 7>, <15, 9>の22である。<0, 9>のように最後が「5」で終わっているものも、最後の一押しが残っているだけなので、問題はない。これらは、<2, 11>, <3, 1>, <3, 9>, <4, 1>, <5, 7>, <6, 3>, <7, 3>, <8, 3>, <8, 7>, <9, 9>, <10, 13>, <12, 5>, <12, 11>, <14, 5>の14である。残ったのは、<2, 7>, <4,15>, <6, 9>, <7, 11>, <13, 11>である。これらは5列が最初、あるいは途中に来ている。これらについて詳しく見てみよう。

<2, 7>: <2, 7>(t5)<1, 3>(t2)<0, 11>(t4)<0, 1>, <4,15>: <4, 15>(t5)<1, 3>(t2)<0, 11>(t4)<0, 1>, <6, 9>: <6, 9>(t1)<4, 15>(t5)<1, 3>(t2)<0, 11>(t4)<0, 1>, <7, 11>: <7, 11>(t5)<3, 11>(t4)<1, 3>(t2)<0, 11>(t4)<0, 1>, <13, 11>: <13, 11>(t5)<13, 1>(t1)<9, 13>(t1)<3, 11>(t4)<1, 3>(t2)<0, 11>(t4)<0, 1>となる。この中で、<6, 9>はいきなり<6, 9>(t1)<4, 15>となり、1回の遷移で既に証明済みの値にまで縮小している。従って、3桁のペアも証明済みの値にまで収縮しているはずである。これ以外の、<2, 7>, <4, 15>, <7, 11>, <13, 11>は最初に5回の列が出現している。これが「奇数効果累積前の一連の連続試行のセット」の間に終了しているのかが問題である。

　<2,7>は、最初の5回のセットの中で、<2, 7>-<3, 11>-<5, 9>-<4, 3>-<6, 5>と遷移している。ここで奇数効果の蓄積が効果を発揮したとすると、<奇数, 13>へと遷移するはずである。この<6, 5>から<奇数, 13>への遷移と、タイプ13の中での処理の中で「割る2」の処理は1+3=4回行われている。<2, 7> = 32+7=39、<6, 5> = 96+5=101、101/39 x 9/16 = 901/714でわずかに拡張しているかも知れない。<4, 15>は、最初の5回のセットの中で、<4, 15>-<7, 7>-<11, 3>-<<1, 0>, 3>-<6, 5>となり、ここで奇数効果の蓄積が効果を発揮すると、<奇数, 13>へと遷移するはずである。この<6, 5>から<奇数, 13>への遷移と、タイプ13の中での処理の中で「割る2」の処理は4回行われている。<4, 15> = 64+15=79、<6, 5> = 96+5=101、101/79 x 9/16 = 909/1264でわずかに縮小して、証明済みの値にまで帰着している。<7, 11>は、<7, 11>-<11, 9>-<8,11>-<13, 1>-<9, 13>となり、ここで奇数効果の蓄積が効果を発揮すると、<偶数, 5>に遷移してしまい、ここで3/16となるので、<7, 11> = 123, <13, 1> = 209, 209/123 x 3/16 = 627/2016で縮小しているので、証明済みの値にまで帰着しているはずである。<13, 11>はどうだろうか。<13, 11>-<<1, 4>, 9>-<15, 7>-<<1, 7>, 3>-<<2, 2>, 13>と遷移している。ここで、奇数効果の蓄積が効果を発揮すると、<偶数, 5>に遷移してしまうので、ここで3/16となる。557/219 x 3/16=1671/3504となり、これも縮小しているので、証明済みの整数にまで縮小していると言える。<2, 7>は、通常ならば「奇数効果累積前の一連の連続試行のセット」の間に最初の5回のセットを消化してしまい、ここで証明済みの値にまで縮小してしまうが、運悪くそうできないで、もう一歩のところで、証明済みの値にまで帰着できない場合は、運が悪いとそこから拡張してしまうこともあり得る。その可能性はかなり小さいと言えるが、起こりえない事ではない。

　ここまでは、「奇数効果累積前の一連の連続試行のセット」を5~6回と考えてきたが、実のところは6回がない(も同然な）のだから、5回ということになる。これは、1回の「奇数効果累積前の一連の連続試行のセット」の間に5/32は確実に1に収束し、1/4は殆どの割合で1に収束すると言ってきたが、この「1/4は殆どの割合で1に収束する」と言ってきた、この「殆ど」の確度がかなり高まったことになる。

　では、合計5回、6回で1に収束するものはどれだけあるか。5回で収束するのは、<0, 7>, <0, 15>, <1, 13>, <3, 13>, <7, 5>, <15, 1>, <15, 5>で、6回で収束するものは、<0, 9>, <1, 3>, <2, 5>, <9, 5>, <10,3>である。これについて少し詳細に見て行こう。

　合計5回のものは、<0, 7>:試行回数　5回、<0, 15>:試行回数　5回、<1, 13>:<1, 13>(t1)<0, 11>(t4)<0, 1> 試行回数　1+4=5回、<3, 13>:　<3, 13>(t1)<1, 7>(t3)<0, 5>(t1)<0, 1> 試行回数　1+(3+1)=5回、<7, 5>:　<7, 5>(t1)<0, 11>(t4)<0, 1> 試行回数　1+4=5回、<15, 1>:　<15, 1>(t1)<11, 5>(t1)<1, 1>(t1)<0, 13>(2)<0, 1> 試行回数　1+(1+(1+2)))=5回、<15, 5>:　<15, 5>(t1)<1, 7>(t3)<0, 5>(t1)<0, 1> 試行回数　1+(3+1)=5回で、合計6回のものは、<0, 9>:　試行回数　6回、, <1, 3>: 　<1, 3>(t2)<0, 11>(t4)<0, 1>　試行回数　2+4=6回、<2, 5>:　<2, 5>(t1)<0, 7>(t5)<0, 1> 試行回数　1+5=6回、<9, 5>:　<9, 5>(t1)<0, 7>(t5)<0, 1> 試行回数　1+5=6回、<10,3>:　<10, 3>(t2)<1, 7>(t3)<0, 5>(t1)<0, 1> 試行回数　2+(3+1)=6回ということになる。<0, 7>, <0, 15>,<0, 9>以外は全て最初の1~2回の試行で起点となる整数よりも小さい値になり、そこで証明済みとなっている。<0, 7>、<0, 15>については2つとも4回目に<0, 5>にまで到達しているのでもう戻りようがない。<0, 5>に到達してしまうと、タイプ5の中で1/16されるので、最後の1歩が足りない状態で、<0, 5>に到達していれば、戻りようがない。場合によっては、桁が1つだけ減少しただけということになることもあるが、その場合でも既に証明済みの整数にまでは縮んでいるはずである。<0, 9>についても最後の1歩が足りない状態で、<0, 13>に分岐した場合には9/16倍されるので確実に1に収束していることになるのは既に説明した通りである。

　従って、ここまでで言えることは、ペアのうち2桁の整数が1~4回で1に収束する場合は、もう片方の3桁のペアは「奇数効果累積前の一連の連続試行のセット」の間に確実に1に収束してしまうことになり、これが20/128。更に2桁のペアが5回までに1に収束してしまう場合はもう一方の3桁のペアは「奇数効果累積前の一連の連続試行のセット」の間にほぼ確実に1に収束するが、これが12/128で、更に5回までの試行の積み重ねの結果1にまで収束しているものは殆ど拡張せずに1に収束すると考えられる。これが、41/128ある。ただし、厳密に言えば<2, 7>は除かなくてはならないと考えると、合計で、(20+12+41-1)/128=72/128=9/16となる。

　残りの7/16についてはどうだろうか。例として<15, 3>を挙げてみると、2回の試行で<8, 9>となり、<8, 9>は1回の試行で<6, 7>となり、<6, 7>は26回の試行で<3, 13>となり、<3, 13>は1回の試行で<1, 7>となり、<1, 7>は3回の試行で<0, 5>となり、<0, 5>は1回の試行で1に収束している。2桁の整数の収束について計算したファイルの中では、これを<15, 3>(t2)<8, 9>(t1)<6, 7>(t26)<3, 13>(t1)<1, 7>(t3)<0, 5>(t1)<0, 1>=34回と表現している。従って、<6, 7>は26回の試行で<3, 13>に遷移する際に極端に拡張してしまうことが予想される。実際の計算では、<<12, 0>, 5>にまで拡張しているので、<6, 7>から<<12, 0>, 5>で、32倍程度になっている。

　では、例として22回以上の拡張傾向の部分が挟まっているものはどれ位あるか数えてみよう。<1, 11>, <1, 15>, <2, 9>, <2, 15>, <3, 7>, <3, 15>, <4, 9>, <5, 3>, <5, 11>, <5, 15>, <6, 1>, <6, 7>, <6, 11>, <6, 13>, <7, 9>, <7, 13>, <8, 1>, <8, 9>, <8, 15>, <9, 1>, <9, 3>, <9,11>, <10, 1>, <10, 5>, <10, 11>, <11, 7>, <12, 1>, <12, 3>, <12, 7>, <13, 7>, <13, 13>, <14, 7>,<14, 11>, <15, 3>, <15, 13>の35例ある。35/128≒1/4位は、操作の途中で極端に大きな値にまで拡張してしまうことが予想される。これ以外の(7-4)/16は収束はなかなか大変だと思われるが、極端に拡張してしまうこともなさそうだということになる。

　複数回の「奇数効果累積前の一連の連続試行のセット」の間ずっと拡張傾向が続くわけではない。例えば、<14, 11>は、<14, 11>(t3)<12, 7>(t5)<5, 15>(t5)<5, 11>(t28)<3, 13>(t1)<1, 7>(t3)<0, 5>(t1)<0, 1>=46回であるが、これは<14, 11>から3回の試行で<12, 7>に遷移し、<12, 7>から5回の試行で<5, 15>に遷移し、<5, 15>から5回の試行で<5, 11>に遷移し、<5, 11>から28回の試行で<3, 13>に遷移し、<3, 13>から1回の試行で<1, 7>に遷移し、<1, 7>から3回の試行で<0, 5>に遷移し、<0,5>から1回の試行で1に収束している。実際には、<5, 11>(t28)<3, 13>ように極端に大きくなってしまう拡大傾向の連続試行のセットは1回現れるだけである。これは理論的にそうなるというよりも、4/16程度の確率なので、1つの2桁の整数が1に収束するまでの間に、それほど頻繁には発生しないだけの話である。例外は、<12, 15>で、<12, 15>(t8)<10, 7>(t18)<3, 13>(t1)<1, 7>(t3)<0, 5>(t1)<0, 1>のように明らかな拡張列の<10, 7>(t18)<3, 13>と、極端な拡張列とは言えないが、「少なくとも拡張気味というべき」<12, 15>(t8)<10, 7>の2つの列が混在している。

　それから、「奇数効果累積前の一連の連続試行のセット」の間に拡張部分セットが含まれているとしても、いきなりそのセットが現れる場合と、2つ目、3つ目、あるいは4つ目あたりで現れる場合では、バスの利用者にとっての利便性が違う。では、1つ目に、拡張列がいきなり現れる場合と、1回目は縮小列であるという場合を分けてみよう。極端に拡大してしまう部分列を含む1/4のうち、1つ目は縮小列だという場合は、<2, 9>（1回目は連続数は1で、2回目が35）、<3, 7>（1つ目は3で、2つ目は34）、<4, 9>（1つ目は1、2つ目は3、3つ目で34）、<5, 3>（1つ目は2で、2つ目が34）、<5, 15>（1つ目は5で、2つ目が28）、<6, 1>（1つ目は1、2つ目が1、3つ目が3で、4つ目が34）、<6, 11>（1つ目は3で、2つ目が28）、<6, 13>（1つ目は1、2つ目は1、3つ目が35）、<7, 9>（1つ目は1で、2つ目が28）、<7, 13>（1つ目は1で、2つ目が34）、<8, 1>（1つ目は1、2つ目は1、3つ目が1、4つ目が3で、5つ目が34）、<8, 9>（1つ目は1、2つ目は26）、<8, 15>（1つ目は5、2つ目は1、3つ目は26）、<9, 1>（1つ目は1、2つ目は1、3つ目は1、4つ目が35）、<9, 3>（1つ目が2、2つ目が2、3つ目が34）、<10, 1>（1つ目が1、2つ目が1、3つ目が28）、<10, 5>（1つ目が1で、2つ目が35）、<10, 11>（1つ目が3、2つ目が1、3つ目が1、4つ目が1、5つ目が35）、その他にも<11, 7>、<12, 1>、<12, 3>、<12, 7>、<13, 7>、<13, 13>、<14, 7>、<14, 11>、<15, 3>、<15, 13>などがある。合計28となる。35/128のうち、28/128は間に極端な拡張列が含まれているが、それが1回目からいきなり現れることはない。35例のうち、1つ目からいきなり「22回以上の拡張傾向の列」が出現するのは、<1, 11>, <1, 15>, <2, 15>, <3, 15>, <5, 11>, <6, 7>, <9,11>の7例だけである。7/128≒8/128＝1/16で、1つ目からいきなり拡張列セットから始まるのは1/16ということになる。ここで「22回以上」としたのは何か確たる事実があって割り出した数字ではない。<0, 3> ~ <15, 15>の収束について具体的に見ると、1に収束するまでに長い拡張列に陥ってしまう場合の例を観察すると、一番大きな値にまで拡張しているのは、最初と最後の1/5程度を除いた、真ん中部分の3/5程度のところであるという漠然とした事実に基づいている。真ん中の3/5程度の部分のどこで最大値になるのかはばらつきがあって明確には分からない。そこで、拡張列を22回とすると、前後の6回ずつを除いて真ん中部分の10回程度の間には、かなりの割合で拡張してしまいそうだということになる。同じような感覚で、「12以上21以下の拡張傾向の列」、「9以上11以下の拡張傾向の列」、「長さ8の拡張傾向の列」に分けて考えることとした。「長さ8の拡張傾向の列」の場合は、前後2回をのぞいて真ん中の「4回分」程度では、それほど拡張しないはずだと考えている。1回目に「12以上21以下の拡張傾向の列」が出現するのは、<6, 15>, <9, 15>, <10, 7>, <13, 15>, <14, 15>である。1回目に「9以上11以下の拡張傾向の列」が出現するのは、<7, 15>, <14, 15>の2つである。ただし、<7, 15>は<7, 15>(t9)<4, 13>(t1)<1, 13>(t1)<0, 11>(t4)<0, 1>なので若干疑問である。<7, 15>(t9)<4, 13>の部分を観察すると、4回目の操作の結果は<<2, 8>, 7>で、5回目の結果は<<3, 12>, 11>で、概算で8倍程度の拡大にとどまっている。更に、「長さ8の拡張傾向の列」が出現するのは、<11, 15>, <12, 15>, <15, 15>で、<12, 15>の場合について具体的に観察すると、<12, 15>(t8)<10, 7>(t18)<3, 13>(t1)<1, 7>(t3)<0, 5>(t1)<0, 1> で、<12, 15>(t8)<10, 7>の途中で、4回目の操作で<<1, 0>, 7>（拡大率は4/3程度）、5日目の操作で<<1, 8>, 11>（拡大率は5/3程度）となり、この辺りで「奇数効果累積前の一連の連続試行のセット」と考えると、それほど拡張していないと言える、少なくとも極端に拡大しているとは言えない。1回目に8以上の拡張傾向の列が現れるのは17/128≒1/8である。1回目に7のセットが現れるのは、<14, 7>の1例、実は1回目に6のセットが現れる場合は1例もない（実は、1回目の<0, 9>の例外を除いて、途中でも6回のセットは一度も出現していない）。

　1回目に現れるセットが「5回以下」の縮小セット場合は、110/128≒112/128=7/8で、殆どの場合は縮小していることになる。1回の「奇数効果累積前の一連の連続試行のセット」が終わると、全く新たに2桁の整数と3桁の整数のペアが生まれることになる。どのようなペアが発生するかは、1回目も、2回目も、それ以降も全く同じ条件で決まる。その都度、同じ条件で3桁の整数が2桁の整数のペアを選ぶと7/8程度の割合で縮小ペアになる。従って、「奇数効果累積前の一連の連続試行のセット」を繰り返していけば確実に1に収束する数を増やしていくことが出来る。

　さて、殆どの場合に7/8は1回目の「奇数効果累積前の一連の連続試行のセット」が終った時点で1以下に収束していると言ったが、残りの1/8はどうだろうか。前の節では、単純に残りの1/8は拡張してしまうと言ったが、もっと詳細に見て行った方が良さそうである。1回の「奇数効果累積前の一連の連続試行のセット」が終わると、全く新たに2桁の整数と3桁の整数のペアが生まれることになる。どのようなペアが発生するかは、1回目も、2回目も、それ以降も全く同じ条件で決まることになる。4回目以内に1に収束してしまう5/32については、たとえそれが2回目の「奇数効果累積前の一連の連続試行のセット」であったとしても、確実に1に収束する。従って、1回目に拡張してしまう1/8のうちの5/32は確実に1に収束するはずである。つまり、2回目の「奇数効果累積前の一連の連続試行のセット」の終わりまでに、7/8 +1/8 x 5/32 = 229/256 は確実に1に収束している。そして、1/8(1- 5/32)=27/256 が若干縮小あるいは少し増加、あるいは極端に拡張かということになる。1/8 x 1/8 = 1/64 = 4/256が極端に拡張なので、残りの23/256は少し増加気味か若干縮小ということになる。ここで、考えておくべきことは、第1回目の「奇数効果累積前の一連の連続試行のセット」と2回目の「奇数効果累積前の一連の連続試行のセット」は全く同じ条件で起きることである。23/256の少し増加気味か若干減少気味の中から極端増加に移る可能性もあるし、極端拡大の中から次の「奇数効果累積前の一連の連続試行のセット」では1に収束してしまうものもある。そして、その割合は、第1回目の「奇数効果累積前の一連の連続試行のセット」でも、2回目の「奇数効果累積前の一連の連続試行のセット」でも、あるいは3回目の「奇数効果累積前の一連の連続試行のセット」でも全く同じである。このように考えると、「奇数効果累積前の一連の連続試行のセット」をどんどん繰り返していけば、その度に1に収束するものが増加していき、最終的に全ての3桁の整数は1に収束することになる。

　以上の考察を元にして実際にどのように1に収束していくか計算してみよう。「奇数効果累積前の一連の連続試行のセット」の1回目は、128 x 1/8 = 16個が1に収束できずに残る。2回目は残り16個のうちの16 x 5/32 = 5/2が1に収束する。従って、残りは16 – 5/2 = (32-5)/2 = 27/2。3回目は27/2 x 5/32 = 135/64 が1に収束する。従って、残りは27/2 – 135/64 = 729/64 ≒ 362/32 = 181/16 ≒ 90/8 ≒ 45/4。4回目は、45/4 x 5/32 = 225/128 ≒ 224/128 = 7/4が1に収束する。従って、残りは45/4 – 7/4 = 38/4 = 19/2。5回目は19/2 x 5/32 = 95/64が1に収束して、残りは9/2 – 95/64 = 187/64 ≒ 192/64 = 3。6回目は、3 x 5/32 = 15/32 が1に収束して、残りは3 – 15/32 = 81/32 ≒ 41/16。7回目は、41/16 x 5/32 = 205/512 ≒ 204/512 = 51/128が1に収束して、残りは41/16 – 51/128 = 277/128 ≒ 276/128 = 138/64 = 69/32。8回目は69/32 x 5/32 = 345/1024 ≒ 336/512 = 21/64 が1に収束して、残りは69/32 – 21/64 = 127/64 ≒ 2。9回目は2 x 5/32 = 10/32 が1に収束して、残りは2 – 10/32 = 27/16。10回目は27/16 x 5/32 ≒ 132/512 = 33/128 が1に収束して、残りは27/16 – 33/128 = 183/128 ≒ 180/128 = 45/32。11回目は45/32 x 5/32 = 225/1024 ≒ 224/1024 = 7/32が1に収束して、残りは45/32 – 7/32 = 38/32。12回目は38/32 x 5/32 = 190/1024 = 188/1024 = 47/512 が1に収束して、残りは38/32 – 47/512 = 561/512 ≒ 560/512 = 35/32。13回目は35/32 x 5/32 = 175/1024 ≒ 172/1024 = 43/256 が1に収束して、残りは、35/32 – 43/256 = 237/256となって、1を切るので、概ね13回目で全ての3桁の整数は1に収束することになる。「奇数効果累積前の一連の連続試行のセット」を5回程度と考えると、概ね65回程度のコラッツ操作で全ての3桁の整数は1に収束することになる。

　残りの5/32は確実に1に収束すると言い切ってしまっていいのだろうか。拡張しても2桁の範囲内なら確実に1に収束することは確かであるが、2桁の整数でも「奇数効果累積前の一連の連続試行のセット」の間に3桁の整数にまで拡大してしまうこともある。それを次のセットに元に戻して更に1にまで収束することができるのかということである。もう少し詳細に見てみよう。1回目は7/8が1に収束し、残りの1/8は拡張してしまう。そして、その残りの1/8のうちの7/8は縮小するが、7/8と言ってもいろいろの場合がある。7/8のうち5/32はかなり縮小して1にまで収束してしまうものもある。8/32は縮小気味である。残りの19/32程は1回目の拡張率当たりにまで戻るだけかもしれない。

　2桁の整数の収束では1に収束したところで計算を止めているが、2回目では更に小さくなるまで計算をするべきである。例えば、<1, 5>は1回の試行で1に収束してしまうが、1回目の「奇数効果累積前の一連の連続試行のセット」が終了した段階で、3桁のペアが拡張して<<<m, n>, 1>, 5>のような形に帰着したとすると、2回目の「奇数効果累積前の一連の連続試行のセット」の最初の試行で3桁の整数に戻り、まだセットが終了するまでに4回の試行の機会が残っているという状態になる。この残りの試行回数4回の機会を利用すると1にまで収束してしまう可能性もある。「奇数効果累積前の一連の連続試行のセット」を5回程度と想定していたので、この5回までにまだ試行の機会が残されている場合がある。これが5/32の意味である。

　それから7/8は縮小し、残りの1/8はひどく拡張する（だろうと思われる）。そして、1/8のうちの7/8は多くはそれほど大きくは拡張しないし、1回目の程度にまで戻るものもあり、更に１まで収束してしまうものもある。そして、1/8 x 1/8 x 1/8 = 1/128 x 1/4 までで、後はずっと拡張し続けるものは考える必要はない。何故なら、2桁の整数は128（正確には<0, 1>を除いて127）通りしかないので、ずっと拡張し続けると言っても、3回目までである。それから、「奇数効果累積前の一連の連続試行のセット」のうちに2回のセットをこなせるものを選んでみよう。3回の試行までに1に収束してしまうものはその後、2回の試行のセットが残されているので、2回目の「奇数効果累積前の一連の連続試行のセット」の中で1に収束してしまうかもしれない。これが13/128 ≒ 12/128 =3/32だけある。

　2回目に1に収束してしまうものが3/32、1回目の起点にまで戻る程度のものが5/32、少し拡張気味なものが17/32、極端に拡張してしまうものが7/32となる。以上に1回目に残った部分の1/8を計算で加えると、2回目に1に収束してしまうものが1/8 x 3/32、1回目の起点にまで戻る程度のものが1/8 x 5/32、少し拡張気味なものが1/8 x 17/32、極端に拡張してしまうものが1/8 x 7/32となる。ここで、1にまで収束してしまうものの合計は7/8 + 3/256 = 227/256で、残りは29/256となる。

　3回目までに1に収束してしまうものはどうなるだろうか。2回の試行までに1に収束してしまうものはその後、3回の試行のセットが残されているので、3回目の「奇数効果累積前の一連の連続試行のセット」の中で1に収束してしまうかもしれない。これが9/128 ≒ 8/128 =2/32だけある。しかし、2回目までのセットの中で元の起点にまで戻る程度のものが、1/8 x 5/32あり、このうちの5/32は1に収束すると考えると、2/32 +1/8 x 5/32 x 5/32 ≒ 1/16で、ここまでに1に収束してしまうものは、227/256 + 1/16 = 241/256で、残りは15/256となる。

　4回目までに1に収束してしまうものはどうなるだろうか。1回の試行で1に収束してしまうものはその後、4回の試行のセットが残されているので、4回目の「奇数効果累積前の一連の連続試行のセット」の中で1に収束してしまうかもしれない。これが3/128 ≒ 1/64だけある。それから、4回目の「奇数効果累積前の一連の連続試行のセット」では、極端に拡張し続けるものはもうないので、2回目までの起点、3回目までの起点にまで戻っている場合の数が少し増えるはずである。このうち、2回目までの起点に戻るものを8/32程度と想定すると、4回目に1に収束してしまうのは1/64 + 1/8 x 8/32 x 5/32 = 5/128で、今までのものと合わせると、241/256 + 5/128 = 251/256となる。残りは、5/256となる。

　5回目になると、2回目までの起点、3回目までの起点、4回目までの起点に戻るものが若干増えて来るはずである。2回目までの起点に戻るものを8/32程度と想定すると、5回目に1に収束するものは、1/8 x 8/32 x 5/32 = 5/1024となり、今までのものと合計すると、251/256 + 5/1024 ≒ 252/256となり、残りは4/256となる。

　6回目になると、2回目までの起点、3回目までの起点、4回目までの起点、5回目までの起点に戻るものが若干増えて来るはずである。2回目までの起点に戻るものを8/32程度と想定すると、6回目に1に収束するものは、1/8 x 8/32 x 5/32 = 5/1024となり、今までのものと合計すると、252/256 + 5/1024 ≒ 1012/1024 = 253/256となり、残りは3/256となる。

　7回目になると、2回目までの起点、3回目までの起点、4回目までの起点、5回目までの起点、6回目までの起点に戻るものが若干増えて来るはずである。2回目までの起点に戻るものを8/32程度と想定すると、7回目に1に収束するものは、1/8 x 8/32 x 5/32 = 5/1024となり、今までのものと合計すると、252/256 + 5/1024 ≒ 1012/1024 = 253/256となり、残りは3/256となる。

　8回目になると、2回目までの起点、3回目までの起点、4回目までの起点、5回目までの起点、6回目までの起点、7回目までの起点に戻るものが若干増えて来るはずである。2回目までの起点に戻るものを8/32程度と想定すると、8回目に1に収束するものは、1/8 x 8/32 x 5/32 = 5/1024となり、今までのものと合計すると、253/256 + 5/1024 ≒ 1016/1024 = 254/256となり、残りは2/256となる。

　9回目になると、2回目までの起点、3回目までの起点、4回目までの起点、5回目までの起点、6回目までの起点、7回目までの起点、8回目までの起点に戻るものが若干増えて来るはずである。2回目までの起点に戻るものを8/32程度と想定すると、9回目に1に収束するものは、1/8 x 8/32 x 5/32 = 5/1024となり、今までのものと合計すると、254/256 + 5/1024 ≒ 1020/1024 = 255/256となり、残りは1/256となる。

　10回目になると、2回目までの起点、3回目までの起点、4回目までの起点、5回目までの起点、6回目までの起点、7回目までの起点、8回目までの起点、9回目までの起点に戻るものが若干増えて来るはずである。2回目までの起点に戻るものを8/32程度と想定すると、10回目に1に収束するものは、1/8 x 8/32 x 5/32 = 5/1024となり、今までのものと合計すると、255/256 + 5/1024 ≒ 1024/1024 = 256/256となり、残りは0となる。「奇数効果累積前の一連の連続試行のセット」を5回と想定すると、50回程度のコラッツ操作の範囲で全ての3桁の整数は1に収束すると言える。

3桁の整数と4桁の整数のペアの収束

　3桁の整数が全て1に収束することが分かれば次は4桁の整数である。4桁の整数に関しては、3桁のペアを選ぶべきか、2桁のペアを選ぶべきか。

　初めに、2桁のペアを選ぶ方法を考えてみよう。末尾2桁が全く同じ4桁の整数と2桁の整数のペアを選ぶ。ここで、4桁の整数の末尾3桁部分と、2桁の整数に着目すると、これは3桁の整数と2桁の整数の末尾2桁が同じペアと同じになる。そして、4桁の整数の第3桁に関しては、3桁の整数と2桁の整数の関係で全て網羅されていることになる。末尾2桁が全く同じ4桁の整数と2桁の整数のペアに対してコラッツ操作を施していくと、4桁の整数の第3桁が奇数の場合の「2で割る」ための調整の際の第2桁への桁下がり、あるいは第2桁から第3桁への桁上がりが発生してその効果が第2桁に蓄積していき、これに並行して、第4桁が奇数の場合の調整のための桁上がり桁下がりの効果が第3桁に積み上がっていくことになる。そして、第4桁の奇数の効果が積み上がって効果を発揮する時、元々の第3桁の偶奇が逆になる。偶数が奇数になるなら「奇数効果累積前の一連の連続試行のセット」の長さが「-1」になる。奇数が偶数になるなら「+1」になる。このことが起きるのは、第4桁が奇数の場合に、第3桁との調整の必要性が発生するためであり、このことが積み重なる結果である。第4桁が奇数になるか偶数になるかは同じ割合だとすると、割合は0.5となる。これが第3桁で積み重なる。この効果が4つ積み重なるためには、コラッツ操作は5回程度必要となる。このタイミングでたまたま3桁と2桁のペアでの第3桁が奇数なら、効果は打ち消しあって偶数となり、たまたま偶数なら奇数となって下位の第2桁への影響が現れる。この結果、第2桁への効果が発現するタイミングが1つだけ「+」になるか「-」になるかということになる。

　このタイミングのずれは、第4桁が奇数か偶数かの割合と、第3桁での効果の蓄積、これが5回程度だということを前提とすると、合わせて7回程度の間に1回だけ起こるはずである。つまり、「奇数効果累積前の一連の連続試行のセット」がコラッツ操作の7回程度に1回だけ少し伸び、また同じ割合で少し縮むことになる。

　「奇数効果累積前の一連の連続試行のセット」を5回程度という前提で話を進めてきたが、ここでもう少し詳細に見てみよう。3桁の整数と2桁の整数のペアの場合、「2で割る」処理を進めるために第3桁が奇数の場合にそれを調整するために第2桁からの桁上がりや第3桁から第2桁への桁下がりが必要となる。そして、第3桁が奇数という状態が3回連続するとそれプラス1（最後の分岐）で合計4回で「奇数効果累積前の一連の連続試行のセット」となる。しかし、3回連続で奇数というのは割合としては少ないだろうということで5回として計算した。それから、第3桁が半分半分の割合で奇数と偶数が出現した時は3+3=6で、6+1=7回位だと思われるが、ここは確実性を高めるために、奇数3回、偶数2回程度で、+1して6回と考えた。ところが、4桁と2桁のペアの場合は、もともとの3桁と2桁のペアの分に、4桁と2桁のペアの分、つまり第4桁の調整分が追加されてくる。そして、第4桁の調整分が累積して奇数効果となる。第4桁の調整分が累積するもまだ奇数効果を発揮するに至らない状態だと、3桁の整数と2桁の整数のペアの場合と同じである。第4桁の調整分の累積が効果を発揮した時、第3桁は偶数なら奇数に、奇数なら偶数になるので、第3桁の調整が少しずれることになる。こうなると、第2桁での効果の発揮もずれることになる。この方法で、5桁、6桁の整数を扱っていくと、どんどんずれが大きくなってしまいそうである。

　4桁の整数と、3桁の整数の下3桁をマッチさせてペアを作る方法ではどうだろうか。4桁の整数と3桁の整数の末尾3桁に関しては、3桁の整数と2桁の整数の末尾2桁が同じ場合で述べたことがそのままそっくり成り立つ。更に、第4桁の「2で割る」ための微調整が第3桁に影響を与えていく様は、3桁の整数と2桁の整数の場合と全く同じなので、「奇数効果累積前の一連の連続試行のセット」の列の長さは同じである。従って、3桁の整数と、2桁の整数の末尾2桁が全く同じペアについて述べたことは、4桁の整数と、3桁の整数の末尾3桁が同じペアにそっくりそのまま当てはまることになる。このことから次のことが言える。2桁の整数について全て1に収束することが分かっているので、3桁の整数についても全て1に収束することが分かる。更に、4桁の整数についても全て1に収束する。このようにして、5桁の整数、6桁の整数、7桁の整数についても全て1に収束することが分かる。従って、どんなに大きな整数でも、それが有限の整数である限り必ず1に収束するということが出来る（証明終わり）。