再々改訂版 2025/05/28
再改定版 2025/05/24
著者 久米原 栄
コラッツ予想とは
コラッツ予想とは、任意の正の整数を選んで、nが偶数なら2で割り、nが奇数なら3を掛けて1を足すという操作を繰り返すと、どんなnから始めても有限回の操作で1に辿り着くという主張である。
証明の要約
任意の正の整数を16を基数としてan16n+an-116n-1+…+a116+a0と表す(an, an-1, … a1, a0は0から15までの整数とする)。ある任意の正の整数に対して、コラッツ操作を施す時に、それが偶数なら、その偶数が含んでいる因数2の個数分「2で割る」処理をして、奇数を取り出すという処理は、コラッツ操作の前処理として考えることにしよう。こうすると、コラッツ操作の対象となるのは奇数ということになる。もちろん、計算処理の途中で偶数が現れることはある。奇数nに対して、(3n+1)/2の処理をして得られた答えに対して、更に「割る2」の処理が可能ならば、「割る2」の処理をして、答えから因数2を取り除くという一連の処理をコラッツ操作1回分として計算することとする。
コラッツ操作の対象を奇数として、16を基数とする表現で表すと、最小桁によってタイプ分けすることが出来る。つまり、あらゆる正の奇数は、タイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15の8つのタイプに分けることが出来る。
任意の整数にコラッツ操作を施すと、タイプ毎に同じ動きをする。そして、あるタイプから別のタイプに遷移する。どのタイプに遷移するかは第2桁が偶数か奇数かによって決定される。このタイプ遷移をグラフに表すことが出来る。これを本稿ではタイプ遷移図と称している。タイプ遷移図はどのタイプからどのタイプに遷移するかをグラフ化したものとなる。あるタイプから別のタイプに移るときにいくつかの分岐先がある。2つに分岐する場合、4つに分岐する場合、8つに分岐する場合である。
2つに分岐するのはタイプ3、タイプ7、タイプ11、タイプ15である。整数にコラッツ操作を施す場合1回の分岐で通常は3/2倍となる。従って、分岐1回で2つに分岐するだけの場合は基本的には3/2倍される。タイプ3、タイプ7、タイプ11、タイプ15を経由するときには基本的に3/2倍されることになる。4つに分岐される時は最初の分岐は(3n+1)/2の処理による分岐で、後の1回の分岐はタイプ内の内部処理として「割る2」されるだけである。従って、4つに分岐する場合は、「3/2 x 1/2 = 3/4」倍されることになり、分岐によって3/4に縮小することになる。4つに分岐するのはタイプ1と、タイプ9である。8つに分岐する場合は最初の(3n+1)/2の処理と、後2回の「割る2」の内部処理になるので、「3/2 x 1/2 x 1/2 = 3/8」となる。8つに分岐するのはタイプ13である。更にタイプ5に関しては内部処理として「1/2 x 1/2 x 1/2」されるので、3/2と合わせると、3/16倍されることになる。そして、タイプ3に関しては、分岐としてタイプ5あるいはタイプ13に分かれるので、拡張タイプでありながらタイプ5、タイプ13の処理と合わせると総合的には縮小タイプとなる事が分かる。以上のことを元にして分岐を辿ると、タイプ1、タイプ3、タイプ5、タイプ9、タイプ13を起点としてコラッツ操作を施すと全て倍率1以下に収束することが分った。そして、タイプ7、タイプ11についても全て倍率1以下になることが証明できた。更に残ったタイプ15についても、それが有限の整数である限り、やがてタイプ7に変容することが証明できた。従って、全ての整数がコラッツ操作の起点となる整数よりも小さい整数にまで収束することが分かった。更に、2桁の整数の全てがコラッツ操作を繰り返すことで1になることも証明した。したがって小さい整数から順番にコラッツ操作を施していくと、全ての整数が1になることが分かった。
以下証明する)
任意の整数は、16を基数として、an16n+an-116n-1+…+a116+a0と表すことが出来る(an,an-1, …a1,a0は0から15までの整数とする)。
ただし、偶数の場合は、2で割ることで、コラッツ操作の出発点となった整数の半分以下になる。コラッツ操作の出発点となる整数を小さい順に選択して1に収束することを証明して行けば、出発点となった整数よりも小さい整数になるということは、その整数は既に証明済みの整数ということになる。したがって、ここから奇数に絞って証明済みの整数にまで収縮することを証明する。
全ての正の奇数は、16p+1, 16p+3, 16p+5, 16p+7, 16p+9, 16p+11, 16p+13, 16p+15と表現して、これをタイプと考えることとする。つまり、全ての数をタイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15に分類し、これらについてコラッツ操作を施してみよう。
コラッツ操作を施した場合のタイプ毎の動き
この節では、16p+nを簡略化して(p, n) あるいは、<p, n>と表記することとする。ここでは、コラッツ操作を行う際の「2で割る」処理を「→」で表現している。2で割る処理が複数回続く時も、単に「→」1個で表現している場合があるので注意してほしい。
ここでは、コラッツ操作の処理途中で、最小桁が偶数の場合は、操作の途中という意味で<p, n>と表現し、最小桁が奇数となり、1回のコラッツ操作が終了した時点で(p, n)という表現を用いている。
● タイプ1
3(p, 1)+1 = <3p, 4>
pが偶数なら、<3p, 4> → <q, 2>
qが偶数なら、<q, 2> → (r, 1)
qが奇数なら、<q, 2> → <q-1, 18> → (r, 9)
pが奇数なら、<3p, 4> → <3p-1, 20> → <q, 10>
qが偶数なら、<q, 10> → (r, 5)
qが奇数なら、<q, 10> → <q-1, 26> → (r, 13)
● タイプ3
3(p, 3) + 1 = <3p, 10>
pが偶数なら、<3p, 10> → (q, 5)
pが奇数なら、<3p, 10> → <3p-1, 26> = (q, 13)
● タイプ5
3(p, 5) + 1 = <3p, 16> = <3p+1, 0> = 16(3p+1) → 3p+1
*<3p+1, 0> はタイプ別で言えば、タイプ0である。操作の途中で最小桁が0になると、<3p+1, 0> = 16(3p+1)+0 = 16(3p+1) → 8(3p+1) → 4(3p+1) → 2(3p+1) → (3p+1)となり、桁の数字が全体として、1桁小さい方にずれることになり、倍率的には<p, 5>が、<0, 3p+1>となっているので、約3/16である。ただし、(3p+1)に因数2が含まれている場合もあり、更に倍率が小さくなる可能性もある。
● タイプ7
3(p, 7) + 1 = <3p, 22>
pが偶数のとき、<3p, 22> → (q, 11)
pが奇数のとき、<3p, 22> = <3p+1, 6> → (q, 3)
● タイプ9
3(p, 9) + 1 = <3p, 28>
pが偶数のとき、<3p, 28> → <q, 14>
qが偶数のとき、<q, 14> → (r, 7)
qが奇数のとき、<q, 14> = <q-1, 30> → <r, 15>
pが奇数のとき、<3p, 28> = <3p+1, 12> → <q, 6>
qが偶数のとき、<q, 6> → (r, 3)
qが奇数のとき、<q, 6> = <q-1, 22> → (r, 11)
● タイプ11
3(p, 11) + 1 = <3p, 34>
pが偶数のとき、<3p, 34> = <3p+2, 2> → (q, 1)
pが奇数のとき、<3p, 34> = <3p+1, 18> → (q, 9)
● タイプ13
3(p, 13) + 1 = <3p, 40>
pが偶数のとき、<3p, 40> = <3p+2, 8> → <q, 4>
qが偶数のとき、<q, 4> → <r, 2>
rが偶数のとき、<r, 2> → (s, 1)
rが奇数のとき、<r, 2> = <r-1, 18> → (s, 9)
qが奇数のとき、<q, 4> = <q-1, 20> → <r, 10>
rが偶数のとき、<r, 10> → (s, 5)
rが奇数のとき、<r, 10> = <r-1, 26> → (s, 13)
pが奇数のとき、<3p, 40> = <3p+1, 24> → <q, 12>
qが偶数のとき、<q, 12> → <r, 6>
rが偶数のとき、<r, 6> → (s, 3)
rが奇数のとき、<r, 6> = <r-1, 22> → (s, 11)
qが奇数のとき、<q, 12> = <q-1, 28> → <r, 14>
rが偶数のとき、<r, 14> → (s, 7)
rが奇数のとき、<r, 14> = <r-1, 30> → (s, 15)
● タイプ15
3(p, 15) + 1 = <3p, 46>
pが偶数のとき、<3p, 46> = <3p+2, 14> → <q, 7>
pが奇数のとき、<3p, 46> = <3p+1, 30> → <q, 15>
以上の考察で、タイプ7、タイプ11、タイプ15については、コラッツ操作を1回施すことで3/2倍となり、第2桁の係数が16を超える場合があるが、このことについては別段の考慮はしていない。もし、第2桁の係数が16を超える場合は、第3桁への桁上がりを考えて<<a2+1, a1>, a0>のような記法を導入すべきかもしれないが、このことについては後で言及することとする。現時点では、タイプの遷移について思考を集中するために、第3桁への桁上がりは、無視している。なぜなら、次に示すタイプ遷移図では、最小桁と、下から2番目の桁の数が決定的に重要だからである。
タイプ遷移図
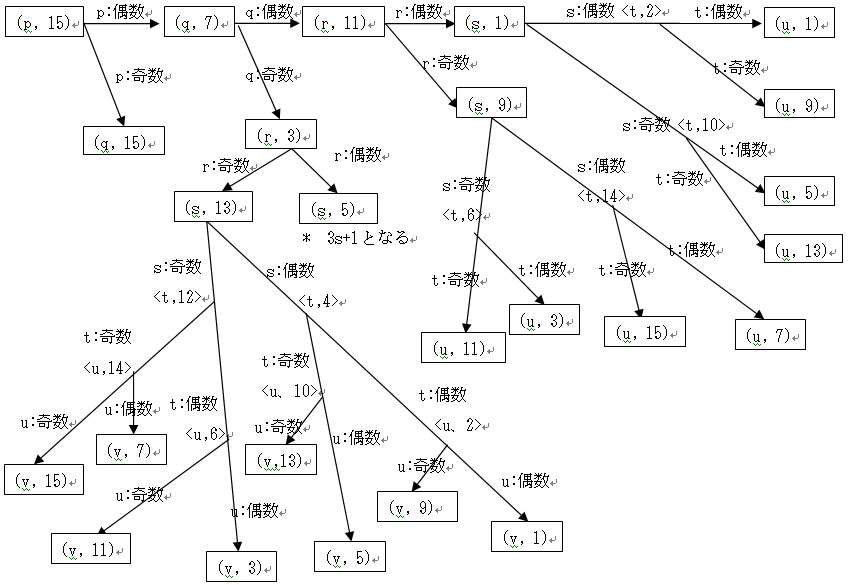
以上の考察を元にしてタイプ遷移図を描くと次のようになる。
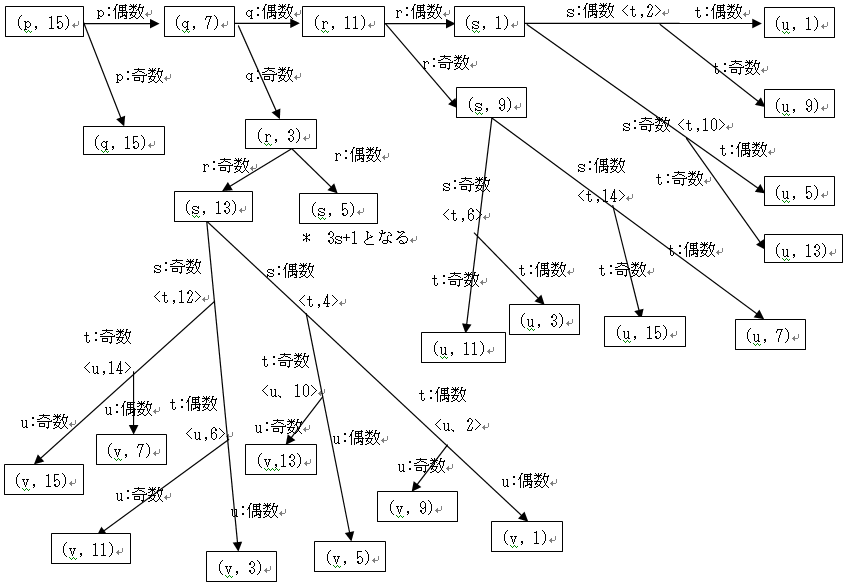
タイプ型と、第2桁の偶数・奇数、3桁以上の整数への拡張
タイプ遷移を考えた場合に、タイプ型と第2桁の偶数・奇数が決定的に重要な働きをすることが分かった。ここまでは、2桁の整数について論じたが、議論を3桁以上の整数にまで拡張したい。
下から2番目の桁の数は「2で割る」という処理をする際の微調整の結果を反映している。最小桁が偶数で、第2桁が奇数の場合の処理については既に説明しているので、ここでは最小桁が偶数で、下から3番目の桁(第3桁)が奇数の場合について考えよう。ここで考えるのは、最小桁が偶数で、第2桁も偶数の場合である。第2桁は、最初から偶数なのか、微調整の結果、偶数になったのかはここでは問わないこととする。第3桁が奇数の場合には、第3桁を「-1」して、第2桁を「+16」するか、第3桁を「+1」して、第2桁を「-16」するかのいずれかである。「2で割る」処理が1回のタイプ3、タイプ7、タイプ11、タイプ15の場合は、「2で割る」処理によって、「+8」あるいは、「-8」という結果が残る。つまり、2桁の整数の処理の結果、第2桁が「m」だったと仮定すると、第3桁との調整を加味した場合は、「m+8」あるいは「m-8」となる。「m」の偶奇と、「m+8」あるいは「m-8」の偶奇は全く同じである。ただし、「m」の偶奇については既に2桁の整数の処理の際に解決しているものとして、ここでは問題としない。ここで、議論しているのは、第3桁からの桁下がり、あるいは第3桁への桁上がりであり、その際の第2桁の「+8」と「-8」である。
「2で割る」処理が2回必要なタイプ1とタイプ9は、最初の「2で割る」処理の際の状況は「2で割る」処理が1回の時と全く同じである。1回目の処理で桁上がりしている場合は「n-8」で、2回目の「2で割る」処理の際に桁上がりがあれば、ここに桁上がりの「-16」を加えて、それを「2で割る」ので、結果は、「n-4-8」となる。ただし、ここでも、nは、2桁のタイプ1とタイプ9の整数に対して「割る2」の処理をした時の第2桁の数字だと仮定している。従って、「-4-8」は、2桁の整数にコラッツ操作をした時と、3桁以上の整数に対してコラッツ操作をした時の差を表していることになる。同じように1回目が桁上がりか、桁下がりか、2回目が桁上がりか、桁下がりかで合わせて「n-4+8」、「n+4-8」、「n+4+8」の4通りの結果が得られる。2回目の「2で割る」処理の際に桁上がり、桁下がりがなければ、「n+4」あるいは「n-4」となる。nの偶数・奇数は、「n-4-8」、「n-4+8」、「n+4-8」、「n+4-8」、「n+4」、「n-4」と同じであることが分かる。
「2で割る」処理が3回必要なタイプ13では、第2桁は2桁の整数として3回目の処理を行った際にsだとすると、「s-2-4-8」、「s-2-4+8」、「s-2+4-8」、「s-2+4+8」、「s+2-4-8」、「s+2-4+8」、「s+2+4-8」、「s+2+4+8」の8通りとなり、あるいは、桁上がり桁下がりがない場合は、「s-2-4」、「s-2+4」、「s+2-4」、「s+2+4」となり、2回目も、3回目も桁上がり桁下がりをしていないとすれば、「s-2」、「s+2」となり、第2桁の偶数・奇数は「s」の場合と同じである。もちろん、タイプ遷移表を見ると、タイプ13は<s, 1>, <s, 9>, <s, 5>, <s, 13>, <s, 3>, <s, 11>, <s, 7>, <s, 15>に分岐し、それぞれの場合について、「s」の値は異なっているが、偶奇については変わりはない。つまり、「s」の偶奇に従って、「s-2-4-8」、「s-2-4+8」、「s-2+4-8」、「s-2+4+8」、「s+2-4-8」、「s+2-4+8」、「s+2+4-8」、「s+2+4+8」、「s-2-4」、「s-2+4」、「s+2-4」、「s+2+4」、「s-2」、「s+2」の偶奇が決まることになる。
以上の考察の結果、3桁以上の整数についても、前の節で説明したタイプ遷移図がそのまま適用できるということになる。
タイプ別の縮小と拡大の概略
タイプ遷移図を見ると、タイプ別の縮小と拡大の概略を知ることが出来る。
上の図では、タイプ遷移の途中の最小桁が偶数の場合については、<>を、1回のタイプ遷移が完了して、最小桁が奇数になった状態を()を使って表現している。□で囲まれた()型のタイプから()型のタイプへの遷移では、コラッツ操作の対象の奇数nに対して、(3n+1)の処理が施され、この結果は必然的に偶数となるため更に2で割る処理が加えられている。従って、基本的に1回のタイプ遷移で対象となった整数は1.5倍されていることになる。ただし、タイプ遷移の間に<>タイプへの処理が介在している場合、すなわちタイプ1、タイプ9、タイプ13では、「2で割る処理」が更に追加されている。タイプ1と、タイプ9では1回、合計で2回、タイプ13では、追加の処理が2回で、合計3回となる。従って、タイプ1とタイプ9では、(3/2)/2=3/4、タイプ13では、((3/2)/2)/2=3/8倍となっている。更にタイプ3はタイプ5、あるいはタイプ13に遷移する。タイプ3から、タイプ5への遷移では3/2となるが、タイプ5内の処理では最低でも3/16倍されている。また、タイプ13への遷移でも、3/2となるが、タイプ13から次のタイプへの遷移で、3/8されている。このように考えると、タイプ1、タイプ3、タイプ5、タイプ9、タイプ13では縮小することが分かる。
拡大するのはタイプ7、タイプ11、タイプ15である。この3つのタイプは(3n+1)/2の処理だけなので、基本的には3/2で拡張するが、タイプ15からタイプ15にループする場合を除いて、全ての場合について起点となった整数よりも小さい値にまで縮小することを証明することが出来た。
これ以降はタイプ15が最終的にタイプ7に移行することについて証明する。タイプ15は最終的にタイプ7に収束することができれば、どのような整数を起点としてコラッツ操作を始めても必ず1に収束することが証明できたことになる。
分岐の仕方を見ると、いくつかの類似点がみられる。例えば、(r, 11)-(s, 1)-(u,1) | (u, 9) | (u, 5) | (u, 13)、(r, 11)-(s, 9)-(u,7) | (u, 15) | (u, 3) | (u, 111)と、(s, 13)-<t, 4>-(v, 1) | (v, 9) | (v, 5) | (v, 13) 、(s, 13)-<t, 12>-(v,3) | (v, 11) | (v, 7) | (v, 15)の分岐が全く同じことが分かる。
また、(r, 3)-(s, 5) | (s, 13)の分岐と、(s, 1)の先の<t, 10>-(u, 5) | (u,13)も同じ、(s, 13)の先の<u, 10>-(v, 5) | (v, 13)も同じである。一見すると、(r, 3)の「3」と<t, 10>, <u, 10>の「10」がマッチしないが、(r, 3)の方は(3n+1)の処理をするので、3×3+1=10となり、マッチする。
(q, 7)-(r, 11) | (r, 3)と、(s, 13)の先の分岐の<u, 6>-(v, 3) | (v, 11)も同じ、(s, 9)の先の分岐の<t, 6>-(u, 3) | (u, 11)も同じである。これについては、(q, 7)の場合は3×7+1=22で、22=1×16+6で、<u, 6>,<t, 6>の「6」とマッチする。
(p, 15)-(q, 7) | (q, 15)も、(s, 9)の先の(t, 14)-(u, 7) | (u, 15)、(s, 13)の先の(u, 14)-(v, 7) | (v, 15)と全く同じである。(p, 15)については、3×15+1=46, 46=2×16+14となり、共に「14」となる。
違いは、タイプからタイプへの遷移では(3n+1)/2の処理が入るが、タイプ内での処理では、「割る2」だけだということである。
偶数・奇数についてもほとんど同じだが、(s, 13)の内部処理で、1番目、3番目は同じで、一番目が奇数の分岐についてのみ2番目は逆になっている。
更にタイプ遷移図を眺めてみると、同じタイプが連続する可能性があることである。それは、タイプ1とタイプ13とタイプ15である。タイプ1から、タイプ1への遷移は4つの選択肢のうちの1つであり、しかもタイプの連続の間に3/4に縮小している。タイプ13からタイプ13への遷移は8つの選択肢のうちの1つであり、しかもタイプの連続の間に、3/8に縮小している。従って、タイプ1とタイプ13の連続については、問題とするには当たらない。問題はタイプ15の連続である。タイプ15は連続する間に1.5倍されるので、例えばタイプ15の連続が100回続くと(100桁の整数の各桁の数字が全て15の場合)、単純にはその間に(1.5)100倍されることになるのだが、事はそれほど単純ではなさそうだ。
15タイプからの遷移
タイプ15は、タイプ7かタイプ15の連続かの1回の選択である。従って、単純に1.5倍される。タイプ15をn回繰り返すと、単純計算では(1.5)n倍で拡大していくことになる。
ここでは、タイプ15の連続から抜け出すことが出来るのかについて議論する。タイプ遷移図を見ると分かる通り、<偶数、15>タイプは次の遷移でタイプ7へ遷移するが、<奇数、15>タイプはタイプ15を繰り返す。
ここからは、an16n+an-116n-1+…+a116+a0を<<<<an,an-1>, an-2>, …, a1>, a0>と表記して計算を行うこととする。ここまでは( )と< >を分けて説明の便宜を図っていたが、これ以降は表現を簡略化する目的で< >と表現することとする。
タイプ15は次のように遷移する。
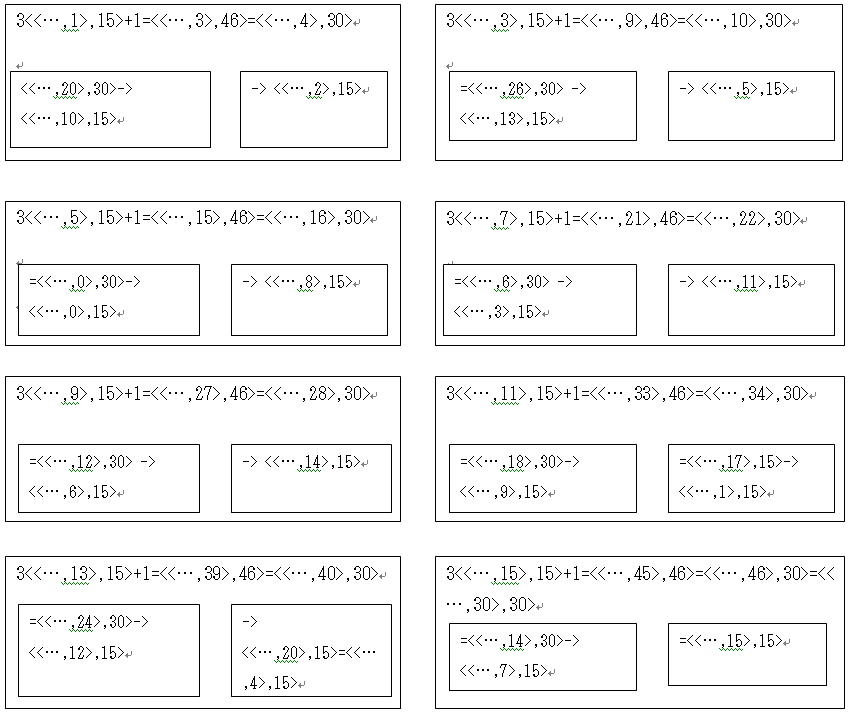
タイプ15でも、<<…, 1>,15>, <<…,5>, 15>, <<…,9>, 15>, <<…,13>, 15>タイプの整数は1回のコラッツ操作で次に、<偶数,15>タイプに遷移しているので、次の操作でタイプ7へと遷移するはずである。
問題は<<…, 3>, 15>, <<…, 7>, 15>, <<…, 11>, 15>, <<…, 15>, 15>タイプである。
このうち、<<…, 3>, 15>と、<<…, 11>, 15>の2つのタイプは問題ない。なぜなら、<<…, 3>, 15>タイプは、次の操作で<<…, 5>, 15>あるいは<<…, 13>, 15>となるので、次の操作で<偶数, 15>タイプとなり、更にその次の操作で、タイプ7へと遷移する。<<…, 11>, 15>も同様に、次の操作で<<…, 1>, 15>あるいは<<…, 9>, 15>タイプへの遷移し、更に次の操作で<偶数, 15>となり、その次にタイプ7へと遷移する。
<<…, 7>, 15>タイプは次の操作で、<<…, 3>, 15>あるいは<<…,11>, 15>タイプとなる。そして、上で説明したように、<<…, 3>, 15>は、<<…, 5>, 15>あるいは<<…, 13>, 15>となり、次の操作で<偶数, 15>となり、更に次の操作でタイプ7へと遷移する。<<…, 11>, 15>についても同じように、<<…, 1>, 15>あるいは<<…, 9>, 15>となり、次に<偶数, 15>タイプとなり、タイプ7への遷移することが出来る。
問題は<<…, 15>, 15>タイプである。このタイプは<<…, 7>, 15>あるいは、<<…, 15>, 15>タイプへ遷移する。<<…, 7>, 15>タイプは既に説明したようにやがてタイプ7へと遷移することが分かっている。
ところが、<<…, 15>, 15>のように15が連続してしまうと、タイプ15から抜け出すことが出来ない可能性がある。次にこの点を確認しよう。
15が最小桁から連続する場合についての考察
15が最小桁から連続する場合は、3n+1の処理をする際の最小桁の45+1=46と、途中桁の46を桁上がりさせる時の上の桁への「+1」が全く同じ動作をしている(45+1=46となり、これが更に上の桁への桁上がりを誘導する)。このため、桁上がりさせた後に元の桁が46-16=30となり、これに対して2で割る処理が加わるため、15となってしまう。
タイプ15の連続からの脱却
各桁の係数が15である場合は一見すると、永遠に1.5倍が続いてしまうように思えるが、そうではない。コラッツ予想では有限の整数を対象としているので、先頭桁というものが必ず存在している。そして、先頭桁の1つ前は0である。つまり、<<<<<<0, 15>, 15>, …>, 15>となっているはずである。これは、<偶数, 15>ということになるので、次のコラッツ操作で、タイプ7へと遷移する。
15タイプから如何にして抜けるかについては、次に図解する。<<<0, 15>, 15>, …>, 15>から、15の並びが1つ減り、15だったところが偶数に変化するまでに4回のコラッツ操作を要していることが分かる。つまり、<<<0, 15>, 15>, …>, 15>は、<<<偶数, 15>, 15>, …>, 15>なので、1回の操作で1つ減り、<<<1, 7>, 15>, …>, 15>になり、ここから<<<…, 偶数>, 15>, …>, 15>に遷移するまでに3回の操作が必要で、合計4回で1つ15の連続列の長さが減ることになる。従って、前に挙げた例の100桁の整数で全ての桁が15の整数の場合は、15の連続から抜け出すまでに、おおよそ(1.5)400倍に拡張することになる。
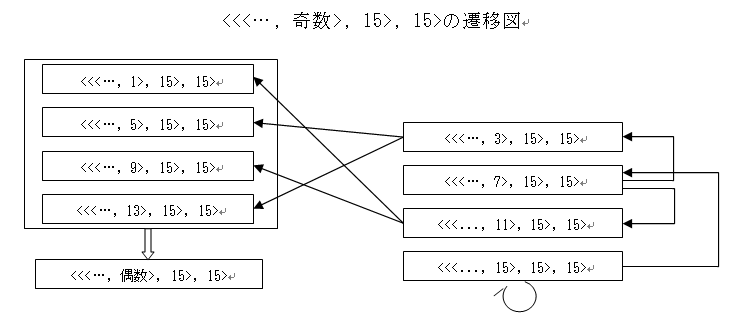
以上、最小桁から15が続いている場合について検討した。
途中にある15についての考察
最小桁から15が連続している場合については厄介であるが、途中で15が出現することもある。これについてはどのように考えたらいいのだろうか。例えば<<<<…, (0から14のいずれか)>, 15>, 15>, (0から14のいずれか)>、…>のような場合である。最小桁が、1、9、13、5のいずれかの場合は、後で2で割る処理が、2回(1と9の場合)、3回(13の場合)、4回(5の場合)あるので、途中にある15は直ぐに他の数に変化してしまう。7、11、15の場合も15の命は短い。そもそも、最小桁から15が続く場合にどうして15が連続してしまうかというと、(3n+1)/2の処理の際の「+1」の処理と同じ作用を、15の桁上がりが果たしてしまうからである。15×3+1=46で、16を桁上がりさせると、最小桁は30となり、その上の桁が45+1=46となり、この桁もさらに上の桁への桁上がりで、30となり、上の桁は45+1=46となって、また桁上がりが発生してしまう。そして、最終的に2で割る処理をすると、30の並びが、全部15へと変わってしまうためである。しかし、途中にある15の場合は、下の桁からの桁上がりがあるとは限らないので、事情が異なる。途中にある15は3倍され、45になるが、下の桁からの桁上がりが期待できないこともある。その場合は、2で割る処理の際に桁間の調整で、46/2=23となり、23=16+7で7になることもあるし、44/2=22となり、22=16+6で6になることもある。あるいはたまたま下からの桁上がりがあって、その結果46になり、更に自分自身が桁上がりして、30になり、2で割る処理で15になることもある。しかし、これもこの時限りのことである。なぜなら、これは2で割る処理が2回の、タイプ7、タイプ11、タイプ15に特有の事情であり、タイプ7は次にタイプ11か、タイプ3となり、タイプ11は次にタイプ1かタイプ9になる。また、タイプ3は次にタイプ5あるいはタイプ13となるので、2で割る処理が1回だけという場合は、ずっと続くわけではないからである。もちろん、タイプ15が最小桁にある場合は例外であるが、これが永遠と続くわけではないことは既に説明したところである。また、今までなかったところに突然15が出現する場合もあるがそれもいつの間にか消滅してしまう。
従って、最小桁から連続している15以外は、途中桁にある15は2、3回のコラッツ操作の間にすぐに消滅してしまうことが分かる。
他のタイプから15タイプへの遷移
15タイプ以外から、15タイプに遷移することがある。タイプ遷移図を見ると、<偶数, 9>-<t, 14>で、tが奇数の時<u, 15>に遷移する。更に、<奇数, 13>-<t, 12>で、tが奇数の時<u, 14>なり、更にuが奇数の時、<v, 15>に遷移している。
<偶数, 9>-<t, 14>(t:奇数)-<u, 15>の遷移では、<0, 9>, <2, 9>, <4, 9>, <6, 9>, <8, 9>, <10, 9>,<12, 9>, <14, 9>のうち、第2桁に因数2が2つ以上入っている<0, 9>, <4, 9>, <8, 9>, <12, 9>はタイプ7へ遷移することが分かる。これに対して、第2桁に因数2が1つしか入っていない<2, 9>, <6, 9>, <10, 9>, <14, 9>はタイプ15を維持する。
3<2, 9> + 1 = <6, 28> → <3, 14> = <2, 30> → <1, 15>
3<6, 9> + 1 = <18, 28> → <9, 14> = <8, 30> → <4, 15>
3<10, 9> + 1 = <30, 28> → <15, 14> = <14, 30> → <7, 15>
3<14, 9> + 1 = <42, 28> → <21, 14> = <20, 30> → <10, 15>
以上より、<2, 9>と<10, 9> だけが、<奇数, 15>となり、15タイプを繰り返すことになる。このうち、<1, 15>はタイプ15の遷移表を確認すると、次のコラッツ操作で<偶数, 15>となり、15タイプから脱出することが出来る。これに対して、<7, 15>は、<<…, 7>, 15>-<<…, 11>, 15> | <<…, 3>, 15>となり、<<…, 11>, 15>-<<…, 1>, 15> | <<…, 9>, 15>, <<…, 3>, 15>-<<…, 5>, 15> | <<…, 13>, 15>となり、<偶数, 15>になるまでに3回のコラッツ操作を必要とし、15タイプを抜けるまでにさらに1回で計4回の操作を必要とする。
<奇数, 13>-<t, 12>(t:奇数)-<u, 14>(u:奇数)の遷移では、<1, 13>, <3, 13>, <5, 13>, <7, 13>, <9, 13>, <11, 13>, <13, 13>, <15,13>のうち<奇数、15>となるのは、<15, 13>のみである。
3<1, 13> + 1 = <3, 40> = <4, 24> → <1, 6> = <0, 22> → <0, 11>
3<3, 13> + 1 = <9, 40> = <10, 24> → <5, 12> = <4, 28> → <1, 7>
3<5, 13> + 1 = <15, 40> = <16, 24> → <2, 3>
3<7, 13> + 1 = <21, 40> = <22, 24> → <11, 12> = <10, 28> → <5, 14> = <4, 30> → <2, 15>
3<9, 13> + 1 = <27, 40> = <28, 24> → <7, 6> = <6, 22> → <3, 11>
3<11, 13> + 1 = <33, 40> = <34, 24> → <17, 12> = <16, 28> → <4, 7>
3<13, 13> + 1 = <39, 40> = <40, 24> → <5, 3>
3<15, 13> + 1 = <45, 40> = <46, 24> → <23, 12> = <22, 28> → <11, 14> = <10, 30> → <5, 15>
<5, 15>はタイプ15の遷移表を確認すると、次のコラッツ操作で<偶数, 15>となり、更に次の操作でタイプ7に遷移することが分かる。
2桁の数について、コラッツ予想が成り立つことの証明
本稿では、小さい整数から順次コラッツ予想が正しいことを証明できていると仮定しているので、ここでは<0, 3>から、<15, 15>までの整数について計算して、<1, 0> → <0, 1>に収束することを示す。証明は、こちらを参照のこと。
<1, 5>を除くと、<0, 3> ~ <15, 15>の全ての奇数は最後に<0, 1>に収束する前に、<0, 5>となり、次の操作で、3<0, 5> + 1 = <0, 16> = <1, 0>となっている。<1, 5>の場合は、3<1, 5> + 1 = <3, 16> = <4, 0> → <1, 0>となる。例外的に<0, 21>は3<0, 21> +1 = 64 → 32 → 16 = <1, 0> → <0, 1>となる。したがって、<0, 3> ~ <15, 15>の全ての整数が<0, 1>に収束する前に一旦<1, 0>になっていることが分かる。この時、最小桁がカットできるので、全体として桁が1つずつ小さい方にずれることになる。
(7)、(11)、(15)でも第2桁が偶数なら縮小傾向に転じる
「タイプの変化による縮小と拡大」では出発点となる整数がタイプ1、(3)、(5)、(9)、(13)の時は必ず縮小して出発点となった整数よりも小さい整数にまで縮小することを証明した。また、出発点がタイプ7、(11)、(15)の時にも、減少傾向列に進む分岐の方が、拡大傾向列の分岐の割合よりも多いことを示し、最終的に倍率1以下にまで収束することを示した。そして、タイプ15についてもいずれタイプ7になることを示した。このことから、どのような整数からを出発点としても、コラッツ操作の結果、出発点となる整数よりも小さい値にまで縮小することが分かった。
今、2桁の整数については、小さい整数から順にコラッツ操作を施した場合は、出発点となった整数よりも小さい値は全て1に収束することが分っている。更に、「タイプの変化による縮小と拡大」で説明したことを3桁の整数に関しても小さい整数の順に当てはめていくと全て出発点となった整数よりも小さく縮んでいくことが分かる。4桁の整数、5桁の整数、6桁の整数でも全く同じである。この方法で、小さい順に順次計算していくと、たとえどんなに大きな整数でも、それが有限の整数、つまり最上位の桁に0が付いている整数である限り、必ず1に収束することが言える。<証明終わり>

コメント