コラッツ操作を行うたびに最下位桁の数値が変化していく。そして、最下位桁の数によってタイプ遷移図上のコースが変化する。ここでは、タイプ遷移図上の分岐を通過する毎に出発点の整数に対してどのように増減していくかを検証し、出発点となった整数に対する倍率を示す。最下位桁の数(タイプ)を(n)で表し、タイプ(n)からタイプ(n+1)への変化を(n)(n+1)と表現することにする。
倍率が1以下になった場合はそこで出発点の整数よりも小さい整数になったものとして検証をやめる。小さい整数から順次コラッツ予想が成立することを証明するという手順で証明を進めているので、出発点よりも小さな値となった時点で証明済みの整数に帰着していることになるからである。
タイプ1の整数を出発点とするとき
(1)(1): 3/4
(1)(5): 3/4
(1)(9): 3/4
(1)(13): 3/4
タイプ1の整数を出発点とする場合は、(1)か(5)か(9)、あるいは(13)に遷移する。いずれの場合も合計で3/4となり、この遷移では必ず証明済みの整数にまで収束する。
タイプ3の整数を出発点とするとき
(3)(5): 3/2 *ただし、(5)の処理の中で3/16となるので、9/32となり縮小する。
(3)(13)(1): 3/2 x 3/8 = 9/16
(3)(13)(3): 3/2 x 3/8 = 9/16
(3)(13)(5): 3/2 x 3/8 = 9/16
(3)(13)(7): 3/2 x 3/8 = 9/16
(3)(13)(9): 3/2 x 3/8 = 9/16
(3)(13)(11): 3/2 x 3/8 = 9/16
(3)(13)(13): 3/2 x 3/8 = 9/16
(3)(13)(15): 3/2 x 3/8 = 9/16
(3)を出発点とした遷移では(5)か(13)に遷移する。(5)に遷移する場合は、(5)の処理の中で、3/16され、合計として9/32となる。(3)を出発点としタイプ13に遷移する場合は、タイプ13の処理の中で3/8されるので、全体として9/16となり、必ず証明済みの整数にまで収束する。なお今後は、(n)の次に(n+1)あるいは(n+3)に分岐する時は表現を簡略化するために、”|”を使って、(n)-(n+1)|(n+3)と書くことがある。
タイプ5の整数を出発点とするとき
(5)の中の処理で3/16されるので、出発点の整数よりも小さい証明済みの整数にまで収束する。
タイプ9の整数を出発点とするとき
(9)(3): 3/4
(9)(7): 3/4
(9)(11): 3/4
(9)(15): 3/4
(9)を出発点とする場合は、このあと(3)、(7)、(11)、(15)のいずれかに遷移し、合計として3/4となり、既に証明済みの整数にまで縮小する。
タイプ13の整数を出発点とするとき
(13)(1): 3/8
(13)(3): 3/8
(13)(5): 3/8
(13)(7): 3/8
(13)(9): 3/8
(13)(11): 3/8
(13)(13): 3/8
(13)(15): 3/8
(13)を出発点とする場合は、(1)、(9)、(5)、(13)あるいは(3)、(11)、(7)、(15)に遷移する。いずれの場合も、タイプ13の処理の中で2回の分岐を行い、それによって割る2の処理を2回しているので、合計で3/2 x 1/2 x 1/2 = 3/8倍されている。従って、いずれの場合も出発点となった整数よりも小さな既に証明済みの整数にまで収束することがわかる。
タイプ7の整数を出発点とするとき
タイプ1、3、5、9、13の整数を出発点とするときは、出発点の整数よりも小さな整数に簡単に帰着することが分かったが、タイプ7、11、15の場合はどうか。タイプ7から確認してみよう。
タイプ遷移図を見ると、タイプ7の整数を出発点とするときは、タイプ3あるいはタイプ11に遷移することが分かる。
タイプ7から出発して、タイプ3を辿る場合は更にタイプ5あるいはタイプ13に遷移する。タイプ5に遷移する場合は、タイプ5の処理の中で3/16されるので、そのことを考慮すると、(7)(3)(5) = 3/2 x 3/2 x (3/16) = 27/64となる。
タイプ7から出発して、タイプ3からタイプ13に至るケースでは、タイプ13の中で3/8されることを考慮すると、次のようになる。
(7)(3)(13)(1): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(3): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(5): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(7): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(9): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(11): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(13): 3/2 x 3/2 x 3/8 = 27/32
(7)(3)(13)(15): 3/2 x 3/2 x 3/8 = 27/32
以上のように、タイプ7からタイプ3に遷移したときはいずれの場合も、出発点の整数よりも小さい値で既に証明済みの整数に帰着することが分かる。
タイプ7から出発してタイプ11を経由する場合は、その後タイプ1か、タイプ9へと分岐する。この分岐では、タイプ7からタイプ11への遷移で、3/2となり、その後タイプ1、タイプ9への遷移で3/2となり、更にタイプ1からタイプ1、5、9、13へと遷移する。タイプ1からタイプ1、5、9、13への分岐で内部的に1/2されていることを考慮すると、3/2 x 3/2 x 3/4 = 27/16となる。
(7)(11)(1)(1): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(1)(5): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(1)(9): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(1)(13): 3/2 x 3/2 x 3/4 = 27/16
タイプ7から11を経由してタイプ9に至る場合も同様である。
(7)(11)(9)(3): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(9)(7): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(9)(11): 3/2 x 3/2 x 3/4 = 27/16
(7)(11)(9)(15): 3/2 x 3/2 x 3/4 = 27/16
これらの中で最後がタイプ1、5、9、13、3で終わっているものについては、内部処理の「割る2」があるので、減少することを簡単に証明することができるかもしれない。中でも最も簡単なのはタイプ5の場合である。タイプ5では内部処理で3/16されるので、その内部処理を考慮に入れると、(7)(11)(1)(5): 27/16 x (3/16) = 81/256となる。更に、タイプ13は内部処理で「割る2」を2回行うので、それを考慮すると、タイプ13から、次の(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への遷移で3/8されることとなるので、(7)(11)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/8 = 81/128となる。
タイプ3に分岐する場合はどうか。タイプ3では、内部処理の「割る2」がないのだが、その後タイプ5あるいはタイプ13に分岐するので大いに期待が持てる。
タイプ5に分岐する場合は次のようになる。
(7)(11)(9)(3)(5): 27/16 x 2/3 x (3/16) = 243/512となる。
タイプ3からタイプ13に分岐する場合は、次に(1)、(3)、(5)、(7)、(9)、(11)、(13)、(15)のいずれかのタイプに分岐する。3から13への分岐で、3/2され、更に13から(1)、(3)、(5)、(7)、(9)、(11)、(13)、(15)のいずれかへの分岐で3/8(= 3/2 x 1/2 x 1/2)されるので、次のようになる。
(7)(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/2 x 3/8 = 243/256
従って、いずれも出発点の整数よりも小さい既に証明済みの整数にまで収束する。
(7)(11)(1)(1)、(7)(11)(1)(9)についても、最後が内部処理で「割る2」を1回行うタイプ1とタイプ9なので少し希望が持てる。
初めに(7)(11)(1)(1)について確認する。
(7)(11)(1)(1)(1): 27/16 x 3/4 = 81/64
(7)(11)(1)(1)(5): 27/16 x 3/4 x (3/16) = 243/1024 *3/16はタイプ5の中の処理
(7)(11)(1)(1)(9): 27/16 x 3/4 = 81/64
(7)(11)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/4 x (3/8) = 243/512 *13からの先の遷移についても考慮に入れている。
(7)(11)(1)(1)(1)と、(7)(11)(1)(1)(9)についてはまだ拡張している。次に、タイプ1は、(1)|(9)|(5)|(13)に分岐し、タイプ9は(7)|(15)|(3)|(11)に分岐している。このことを考慮すると次のようになる。
(7)(11)(1)(1)(1)(1): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(1)(5): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(1)(9): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(1)(13): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
タイプ9からの分岐についても同じようになる。
(7)(11)(1)(1)(9)(3): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(9)(7): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(9)(11): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
(7)(11)(1)(1)(9)(15): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256
次に、(7)(11)(1)(9)についても検討する。タイプ9はその後、(7)|(15)|(3)|(11)へと分岐する。(7)、(11)、(15)は拡張してしまうが、(3)への分岐は縮小するので、(7)(11)(1)(9)(3)について検討してみよう。タイプ3はその後タイプ5あるいはタイプ13に分岐する。
タイプ5への分岐
(7)(11)(1)(9)(3)(5): 27/16 x 3/4 x 3/2 x (3/16) = 729/2048
タイプ13への分岐はその後、(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)へと分岐し、その時内部処理で3/8されるので、次のようになる。
(7)(11)(1)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/4 x 3/2 x 3/8 = 729/1024
この結果、(7)(11)(1)(9)(7)と、(7)(11)(1)(9)(11)、(7)(11)(1)(9)(15)が残ったことになる。更に、(7)(11)(9)(7)、(7)(11)(9)(11)、(7)(11)(9)(15)が残っている。(7)(11)(1)(9)(7)についてはタイプ7に戻ってしまったので、今まで計算したことがそのまま繰り返されることになる。例えば、(7)(11)(1)(9)(7)の後に収束傾向の列が続いたとしても、それが(11)(1)(1)(9)(7)の場合は、 (7)(11)(1)(1)(9)(7): 27/16 x 3/4 x 3/4 = 81/64 x 3/4 = 243/256で縮小傾向がそれほど大きくないので合計で、81/64 x 243/256 = 19683/16384となり、拡張傾向から脱却できない。(7)(11)(1)(9)(7)の後に、(11)(1)(9)(3)(13)が続くと、(7)(11)(1)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 27/16 x 3/4 x 3/2 x 3/8 = 729/1024なので、合計81/64 x 729/1024 = 59049/66176となって、出発点よりも小さな証明済みの整数以下に収束する。
タイプ11の整数を出発点とするとき
タイプ11はその後タイプ1か、タイプ9に遷移する。タイプ11から、タイプ1、タイプ9への遷移の倍率はいずれも3/2で増加する。しかし、タイプ1から(1)、(5)、(9)、(13)、タイプ9から(3)、(7)、(11)、(15)に遷移し、いずれの場合も3/2 x 1/2 = 3/4となる。従って合計で3/2 x 3/4 = 9/8となり、わずかに増加している。
(11)(1)(1): 3/2 x 3/4 = 9/8
(11)(1)(5): 3/2 x 3/4 = 9/8
(11)(1)(9): 3/2 x 3/4 = 9/8
(11)(1)(13): 3/2 x 3/4 = 9/8
(11)(9)(3): 3/2 x 3/4 = 9/8
(11)(9)(7): 3/2 x 3/4 = 9/8
(11)(9)(11): 3/2 x 3/4 = 9/8
(11)(9)(15): 3/2 x 3/4 = 9/8
タイプ11の整数が出発点の場合は、いずれもわずかに拡張している。従って、この後に、縮小傾向のタイプ1、タイプ3、タイプ5、タイプ9、タイプ13が続くときは簡単に縮小してしまうことが容易に予想される。なぜなら、タイプ1、タイプ9の場合は内部の分岐で1/2がそれぞれ1回となり、タイプ間の遷移分を合わせて3/2 x 1/2 = 3/4されるので、出発点のタイプ11からの分と合計で、9/8 x 3/4 = 27/32となるからである。タイプ13では、内部処理の分岐が2回あるので1/4となり、タイプ5ではタイプ内の処理で3/16される。また、タイプ3の場合は内部での分岐はないが、その後タイプ5あるいはタイプ13に分岐するので、それらの分を合計すると十分に1以下に収束することが予想されるからである。では実際に確認してみよう。
(11)(1)(1)(1): 9/8 x 3/4 = 27/32
(11)(1)(1)(5): 9/8 x 3/2 x (3/16) = 81/256
(11)(1)(1)(9): 9/8 x 3/4 = 27/32
(11)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 9/8 x 3/4 x 3/4 x 3/8 = 243/1024
(11)(1)(5): 3/2 x 3/4 x (3/16) = 27/128
(11)(1)(9)-(7)|(15)|(3)|(11): 9/8 x 3/4 = 27/32
(11)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 9/8 x 3/2 x 3/8 = 81/128
(11)(9)(3)(5): 9/8 x 3/2 x (3/16) = 243/512
(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 9/8 x 3/2 x 3/8 = 81/128
残ったのは(11)(9)(7): 3/2 x 3/4 = 9/8、(11)(9)(11): 3/2 x 3/4 = 9/8、(11)(9)(15): 3/2 x 3/4 = 9/8である。いずれも、タイプ7、タイプ11、タイプ15で終わっている。
タイプ15の整数を出発点とするとき
タイプ15の整数を出発点とする場合は、それに続く遷移はタイプ7かタイプ15である。タイプ15の連続については別に考える必要があるので、ここではタイプ15からタイプ7への遷移についてのみ検討する。タイプ15からタイプ7への遷移では3/2に拡大する。タイプ7からの遷移については既に検討済みである。(7)(11)(1)(9)(7)と、(7)(11)(1)(9)(11)、(7)(11)(1)(9)(15)、(7)(11)(9)(7)、(7)(11)(9)(11)、(7)(11)(9)(15)については拡張しているので、最初にタイプ15からタイプ7への遷移で出発している場合は、更に3/2されるので、合計で拡張されることになる。(7)(11)(1)(9)(7)と、(7)(11)(1)(9)(11)、(7)(11)(1)(9)(15)、(7)(11)(9)(7)、(7)(11)(9)(11)、(7)(11)(9)(15)以外については縮小していることが分かっている。しかし、15から7に遷移する過程で既に3/2されているので、これを打ち消すほどに縮小していなくては全体として縮小しているとは言えない。つまり、タイプ15から出発した場合は、タイプ7から出発した場合と比較して、最初に3/2倍される分だけ、縮小が難しいということになる。
では実際に確認してみよう。
(15)(7)(3)(5): 3/2 x 3/2 x 3/2 x (3/16) = 81/128 *ただし、3/16はタイプ5内の処理
(15)(7)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/8 = 81/64
(15)(7)(11)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 = 81/32
(15)(7)(11)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 = 81/32
(15)(7)(3)(5)以外は全部拡大しているので、その後の分岐を検討する必要がある。
(15)(7)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)について検討する。タイプ13の次に(1)|(3)|(5)|(9)|(13)に分岐する時は減少に転じるので、出発時点の整数よりも小さい整数にまで縮小するかについて検討してみよう。簡単そうなものは、(5)|(3)|(13)の時である。
(15)(7)(3)(13)(5): 81/64 x (3/16) = 243/1024 *タイプ5の内部での処理を追加した
となり、(5)が続く時は出発点となった整数よりも小さい整数にまで帰着する。
(15)(7)(3)(13)(3)については、その後(5)|(13)が続くので、それぞれについて確認してみよう。
(15)(7)(3)(13)(3)(5): 81/64 x 3/2 x (3/16) = 729/2048
(15)(7)(3)(13)(3)(13): 81/64 x 3/2 x (3/8) = 729/1024
となり、いずれも出発点となった整数よりも小さな整数にまで収束している。次に(15)(7)(3)(13)-(1)|(9)について検討する。
(15)(7)(3)(13)(1)-(1)|(5)|(9)|(13): 81/64 x 3/4 = 243/256となる。(5)は更に内部処理で3/16され、(13)はその次の(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への遷移で更に3/8され、(1)|(9)では次の遷移で更に3/4されることになるが、243/256となった時点で、出発点の整数よりも小さくなっているので、ここまでで十分である。
(15)(7)(3)(13)(9)-(3)|(7)|(11)|(15): 81/64 x 3/4 = 243/256となり、いずれも出発点となった整数よりも小さい整数にまで収束している。しかし、(15)(7)(3)(13)-(7)|(11)|(15)については、いずれも拡大してしまうのでこれに続く列に関する検討は取り敢えず保留としておく。
次に、(15)(7)(11)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 = 81/32と、(15)(7)(11)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 = 81/32について検討する。(15)(7)(11)(1)-(1)|(5)|(9)|(13)については4つの場合がすべて縮小傾向であるので、一旦拡張してしまった81/32をどこまで縮小させることができるかが問題となる。
(15)(7)(11)(1)(5)については、タイプ5の中の処理で3/16される。
(15)(7)(11)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x (3/16) = 243/512
となり、一気に出発点の整数よりも小さな証明済みの整数にまで縮小する。
(15)(7)(11)(1)(13)についてもタイプ13から次の(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への遷移で3/8されるので、かろうじて出発点の整数よりも収縮することになる。
(15)(7)(11)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/8 = 243/256
(15)(7)(11)(1)(1)については、更に(1)|(5)|(9)|(13)のいずれかに分岐するが3/4なので一気に出発点の整数よりも小さくなることは難しい。同じことは、(15)(7)(11)(1)(9)についても言える。(15)(7)(11)(1)(9)はその後(7)|(15)|(3)|(11)のいずれかに分岐し、拡大率は3/4である。
(15)(7)(11)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128
(15)(7)(11)(1)(9)-(7)|(15)|(3)|(11): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128
(15)(7)(11)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128については、-(1)|(5)|(9)|(13)がいずれも縮小傾向なので、このまま処理を続けると、全体として1以下になることが期待できる。
初めに簡単そうなタイプ5、タイプ13が続く場合について確認していく。タイプ5についてはタイプ内の処理で3/16になるので、タイプ内での処理を考慮に入れると、このままで(15)(7)(11)(1)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x (3/16)= 243/128 x (3/16) = 729/2048となる。13が続く場合は、タイプ13から-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)への分岐で3/8されるので、(15)(7)(11)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/8 = 243/128 x 3/8 = 729/1024となる。これに対して、タイプ1とタイプ9が続く時については、少し難しそうである。1回の延長では3/4されるだけなので、この処理を2回、3回と続ける必要がありそうである。では実際に計算してみよう。
(15)(7)(11)(1)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 = 729/512
まだだめであるが、タイプ5と13が続く時は、容易である。タイプ5が続く時はタイプ内の処理を考慮に入れるだけで問題は解決する。(15)(7)(11)(1)(1)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x (3/16)= 243/128 x 3/4 x (3/16) = 729/512 x (3/16) = 2187/8192となり出発点の整数よりも小さな証明済みの整数にまで収束する。
(15)(7)(11)(1)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/8 = 243/128 x 3/4 x 3/8 = 729/512 x 3/8 = 2187/4096となって、出発点の整数よりも小さな証明済みの整数にまで収束する。ではタイプ1とタイプ9が続く時はどうか確認してみよう。ともに3/4倍されるだけなので微妙な数字になりそうである。
(15)(7)(11)(1)(1)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 = 729/512 x 3/4 = 2187/2048となり、僅かながら倍率1以下にまでは届かない。
この場合も、タイプ5とタイプ13が続く時は簡単である。問題は、タイプ1とタイプ9が続く時である。しかし、既に2187/2048にまで辿り着いているので、更に3/4倍することで倍率1以下にまで届きそうである。ここでも、タイプ5とタイプ13が続く場合は容易である。
(15)(7)(11)(1)(1)(1)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x (3/16) = 243/128 x 3/4 x 3/4 x (3/16) = 729/512 x 3/4 x (3/16) = 2187/2048 x 3/16 = 6561/32768となり、タイプ5内の内部処理を追加しただけで、倍率1以下にまで収束した。
タイプ13については、次に-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15)が続く。では計算してみよう。
(15)(7)(11)(1)(1)(1)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/8 = 243/128 x 3/4 x 3/4 x 3/8 = 729/512 x 3/4 x 3/8 = 2187/2048 x 3/8 = 6561/16384となり、こちらも倍率1以下にまで縮小している。
さて問題のタイプ1とタイプ9の場合であるが、こちらは既に後一歩のところまで縮んでいるので、3/4で十分である。
(15)(7)(11)(1)(1)(1)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
(15)(7)(11)(1)(1)(1)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
となって、いずれも倍率1以下にまで収束している。
(15)(7)(11)(1)(1)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4 x 3/4 = 729/512 x 3/4 = 2187/2048については、減少傾向にあるタイプ3についてだけ検証し、残りの(15)(7)(11)(1)(1)(1)(9)-(7)|(11)|(15)については保留とする。
(15)(7)(11)(1)(1)(1)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/2 x (3/16) = 243/128 x 3/4 x 3/4 x 3/2 x (3/16) = 729/512 x 3/4 x 3/2 x (3/16) = 2187/2048 x 3/2 x (3/16) = 19683/65536
(15)(7)(11)(1)(1)(1)(9)(3)(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/4 x 3/2 x (3/8) = 243/128 x 3/4 x 3/4 x 3/2 x (3/16) = 729/512 x 3/4 x 3/2 x (3/16) = 2187/2048 x 3/2 x (3/16) = 19683/32768
(15)(7)(11)(1)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 = 243/128 x 3/4についてもタイプ3について検討し、(15)(7)(11)(1)(1)(9)-(7)|(11)|(15)については保留する。
(15)(7)(11)(1)(1)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/2 x (3/16) = 243/128 x 3/4 x 3/2 x (3/16) = 6561/16384となり、倍率1以下にまで収束している。
(15)(7)(11)(1)(1)(9)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/4 x 3/2 x (3/8) = 243/128 x 3/4 x 3/2 x (3/8) = 6561/8192となり、倍率1以下にまで収束している。
(15)(7)(11)(1)(9)-(7)|(15)|(3)|(11): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 = 243/128については、タイプ3が続く場合について検証し、(15)(7)(11)(1)(9)-(7)|(15)|(11)については保留とする。
(15)(7)(11)(1)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/2 x (3/16) = 243/128 x 3/2 x (3/16) = 2187/4096となり、倍率1以下にまで収束している。
(15)(7)(11)(1)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/4 x 3/2 x (3/8) = 243/128 x 3/2 x (3/8) = 2187/2048となり、惜しくも倍率1以下にまでは達していない。しかし、(5)が続く時は内部処理で3/16で、(13)についてはこの後3/8、(1)|(9)については3/4、(3)についてはこの後(5)、(13)に分岐するので、倍率1以下にまで到達することになる。(15)(7)(11)(1)(9)(3)(13)-(7)|(11)|(15)のように(7)|(11)|(15)が続く時は保留とする。
(15)(7)(11)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 = 81/32についても、(15)(7)(11)(1)-(1)|(5)|(9)|(13)と同様の処理が行われることとなる。こちらは、縮小傾向のタイプ3のみを検証する。(15)(7)(11)(9)-(7)|(11)|(15)については更に拡大してしまうので、これ以降の列に関する検討は保留する。
(15)(7)(11)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x (3/16) = 81/32 x 3/2 x (3/16) = 729/1024となり、倍率が1以下にまで集束することが分った。
(15)(7)(11)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 = 729/512となり、倍率1以下にはまだ届いていない。(5)と(3)から(13)へと続く時は容易であることが予想されるが、(1)と(9)についてはギリギリで届かない。では実際に確認しよう。
(15)(7)(11)(9)(3)(13)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x (3/16) = 81/32 x 3/2 x 3/8 x (3/16) = 729/512 x (3/16) = 2187/8192
(15)(7)(11)(9)(3)(13)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x (3/16) = 81/32 x 3/2 x 3/8 x 3/2 x (3/16) = 729/512 x 3/2 x (3/16) = 6561/16384
(15)(7)(11)(9)(3)(13)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/2 x 3/8 = 729/512 x 3/2 x 3/8 = 6561/8192
(15)(7)(11)(9)(3)(13)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/8 = 81/32 x 3/2 x 3/8 x 3/8 = 729/512 x 3/8 = 2187/4096
(15)(7)(11)(9)(3)(13)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/4 = 81/32 x 3/2 x 3/8 x 3/4 = 729/512 x 3/4 = 2187/2048となってわずかに届かない。しかし、いずれも縮小列が続いているのでもうすぐである。
(15)(7)(11)(9)(3)(13)(1)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/4 x (3/16) = 81/32 x 3/2 x 3/8 x 3/4 x (3/16) = 729/512 x 3/4 x (3/16) = 2187/2048 x (3/16) = 6561/32768 *タイプ5の内部処理を追加
(15)(7)(11)(9)(3)(13)(1)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/4 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/8 = 729/512 x 3/4 x 3/8 = 2187/2048 x 3/8 = 6561/16384
(15)(7)(11)(9)(3)(13)(1)(1)-(1)|(5)|(9)|(13): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
(15)(7)(11)(9)(3)(13)(1)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/4 = 729/512 x 3/4 x 3/4 = 2187/2048 x 3/4 = 6561/8192
(15)(7)(11)(9)(3)(13)(9)-(3)|(7)|(11)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 = 729/512 x 3/4 = 2187/2048となり、こちらもわずかに届かない。こちらは(3)が続く場合だけ検証し、ー(7)|(11)|(15)が続く、(15)(7)(11)(9)(3)(13)(9)-(7)|(11)|(15)については保留として残す。
(15)(7)(11)(9)(3)(13)(9)(3)(5): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x (3/16) = 81/32 x 3/2 x 3/8 x 3/4 x 3/2 x (3/16)= 729/512 x 3/4 x 3/2 x (3/16)= 2187/2048 x 3/2 x (3/16) = 19683/65536
(15)(7)(11)(9)(3)(13)(9)(3)(13)-(1)|(3)|(5)|(7)|(9)|(11)|(13)|(15): 3/2 x 3/2 x 3/2 x 3/4 x 3/2 x 3/8 x 3/2 x 3/8 = 81/32 x 3/2 x 3/8 x 3/4 x 3/2 x 3/8= 729/512 x 3/4 x 3/2 x 3/8= 2187/2048 x 3/2 x 3/8 = 19683/32768
(15)(7)(11)(9)(3)(13)-(7)|(11)|(15)については保留とする。
保留として残したものについての検討
今までの検討の結果、保留として残したのはタイプ7で始まる(7)(11)(1)(9)-(7)|(11)|(15)、(7)(11)(9)-(7)|(11)|(15)と、タイプ11で始まる(11)(9)-(7)|(11)|(15)と、タイプ15で始まる(15)(7)(3)(13)-(7)|(11)|(15)、(15)(7)(11)(1)(1)(1)(9)-(7)|(11)|(15)、(15)(7)(11)(1)(1)(9)-(7)|(11)|(15)、(15)(7)(11)(1)(9)(3)(13)-(7)|(15)|(11)、(15)(7)(11)(1)(9)-(7)|(15)|(11)、(15)(7)(11)(9)(3)(13)(9)-(7)|(11)|(15)、(15)(7)(11)(9)(3)(13)-(7)|(11)|(15)、(15)(7)(11)(9)-(7)|(11)|(15)と、(15)の連続である。いずれもタイプ7、タイプ11、あるいはタイプ15で始まり、タイプ7、タイプ11、タイプ15で終わっている列である。タイプ7、タイプ11、タイプ15で始まる列が全て拡大列というわけではないことは今までの検証で分かった。
保留として残したものが全体のでの程度あるかを求めてみよう。タイプ1、3、5、9、13で出発した列は全て倍率1以下にまで集束することが分った。つまり、5/8は直ちに収束する。これに対して、タイプ7、タイプ11、タイプ15から出発した整数列は直ちに収束するとは限らないことが分かった。3/8のうちどの程度が拡散列として残るのか計算してみよう。

上の図のように倍率1以下に確実に収縮することを示せたのは1/4 + 1/4 + (1/64) x 4 + 1/64 + 1/16 + 1/64 + 1/16 = 49/64で、最初にタイプ7が選ばれるのは、1/8なので、それを合わせると1/8 x 15/64 = 49/512ということになる。拡大基調にあるとして保留としたのは15/64で、最初にタイプ7が選択される場合の1/8を考慮に入れると、15/512となる。
次に最初に11が来る場合について考えてみよう。

倍率1以下に確実に収束することを示せたのは(1/8) x 4 + (1/16) x 2 = 5/8で、最初にタイプ11が来るのは1/8の割合なので合わせて、5/64ということになる。拡大基調だとして保留したのは1/8 x 3/8 = 3/64ということになる。
次にタイプ15から開始される場合について計算してみよう。
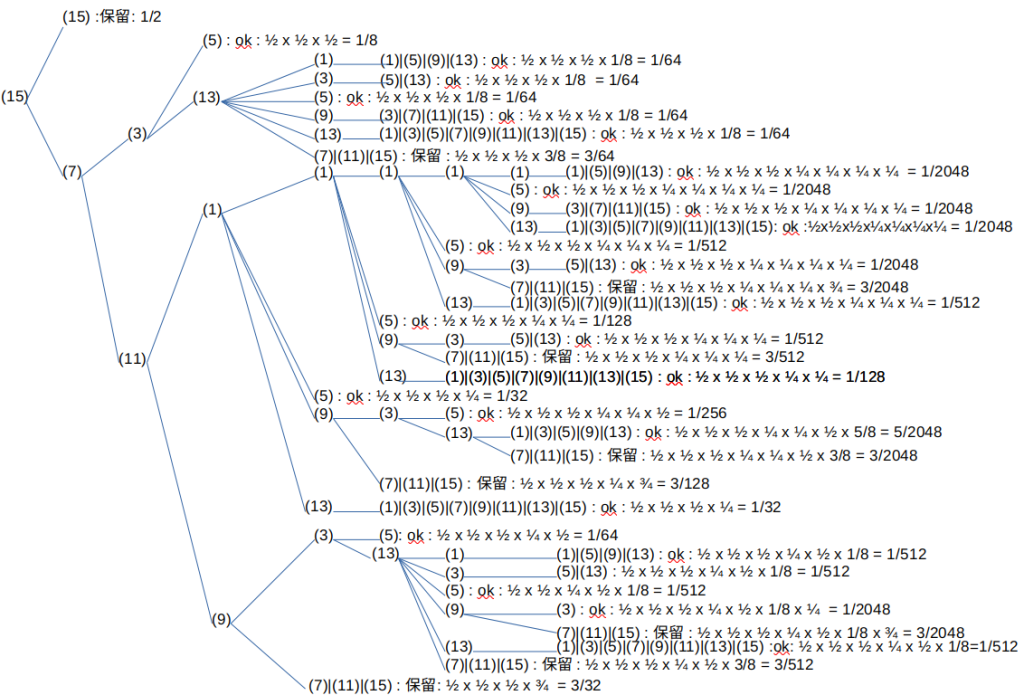
タイプ7の前にタイプ15が追加されているだけなのにタイプ7の図と比較すると格段に複雑になっていることがすぐに分かる。タイプ15が先頭に来ることで最初に3/2倍されることになる。従って、その後に縮小列が続くとしても、必ずしも最初の3/2の影響を払拭することができないため、タイプ7が最初に来る場合と比較して難しくなるためである。
では、タイプ15が先頭に来る場合の計算をしてみよう。初めに、(7)|(15)に分岐して、分岐15は保留となる。タイプ7が続く時は1/2倍となる。保留となる場合を足していくと、1/2 + 3/64 + 3/2048 + 3/512 + 3/2048 + 3/128 + 3/2024 + 3/512 + 3/32 = 1393/2048となり、最初にタイプ15が来る割合は1/8なので、全体として1393/16384となる。
タイプ7から出発したときの保留の率は15/512、タイプ11から出発したときの保留の率は3/64、タイプ15から出発したときの保留の率は1393/16384となる。これらを合計すると15/512 + 3/64 + 1393/16384 = (480 + 768 + 1393)/16384 = 2641/16384 = 0.161193848 ≒0.16 = 4/25となる。
以上の計算結果を踏まえると、保留として残したタイプの列に更にコラッツ操作を追加するとどうなるか考えてみよう。最初にタイプ1、タイプ3、タイプ5、タイプ7、タイプ9、タイプ11、タイプ13、タイプ15のいずれかの整数で出発する。それぞれの割合は1/8ずつである。そして、タイプ1、タイプ3、タイプ5、タイプ9、タイプ13で出発した整数は全て出発点の整数よりも小さな整数にまで収束し、その時点で証明済みに整数にまで縮んだことになる。割合としては、5/8である。これに対して、タイプ7で出発した整数は、15/64が出発点の整数にまで縮まりきらない。タイプ7で出発する割合と合わせると15/512が出発点の整数よりも拡大してしまうことになる。タイプ11で出発した整数は、3/8が拡大してしまう。タイプ11で始まる割合の1/8と合わせると、3/64ということになる。タイプ15は拡大の割合が極めて高い。それはタイプ15からタイプ15へと戻ってしまう割合が1/2あるからである。総合すると、1393/2048あり、更にタイプ15で出発する割合である1/8を掛け合わせると1393/16384となる。
タイプ7、タイプ11、タイプ15で始まる場合で拡大基調で終わっている場合は、全てタイプ7、タイプ11、タイプ15で終わっている。これらについて更にコラッツ操作を継続すると最初の計算とは少し違ってくる。最初の計算では全体として21/25は減少傾向で、4/25は更に拡大するという結果が得られたが、次はこの4/25に対してはタイプ7、タイプ11、タイプ15に対するコラッツ操作のみが継続されるからである。
タイプ7からは(3)あるいは(11)に分岐して、(3)は縮小傾向である。タイプ11からは(1)あるいは(9)に分岐していずれも縮小傾向である。これに対してタイプ15は(7)あるいは(15)に分岐していずれも拡大傾向である。
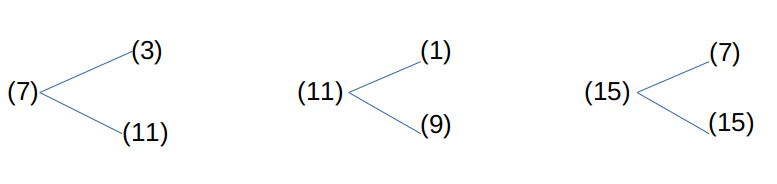
拡大傾向の列に後続の列を続けてみると次のようになる。
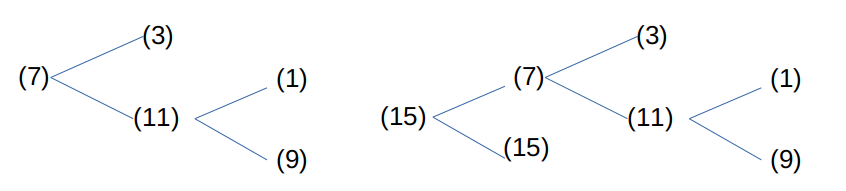
(15)が連続する場合以外は、減少傾向の列が続くことになる。もちろん、減少傾向の列が続いても直ちに倍率1以下になるとは言えない。一旦拡大してしまっているので、単純な計算はできないからである。例えば、(7)で終わっている列に続いて、(11)(9)と続くと縮小するが、(9)の後に更に-(7)|(11)|(15)が続いてしまうとまた拡大してしまうし、(11)(9)(3)と続いたとしても倍率1以下にまで縮小してしまうとは断言できない。拡大傾向の列に後続の列が続いている場合、それが縮小傾向の列だとしても、今までの列の倍率を打ち消して倍率1以下にまで持っていけるかどうかが重要となってくる。
上に上げた図ではタイプ7で終わっている場合の次の分岐はどうなるかという観点から見たが、タイプ7で終わっている場合が果たしてタイプ7で始まっているのか、あるいはタイプ11か、はたまたタイプ15なのかは分からない。タイプ7、タイプ11、タイプ15を一緒にして考えるしかなさそうである。
では、(15)の連続についてはどうか。単純計算すると(15)の連続が1000回続けば倍率は(1.5)1000となる。10000回続けば、100000回続けば、その間は拡大し続けることになる。この連続をいつか断ち切れることができるかが重要となる。


コメント